
题目列表(包括答案和解析)
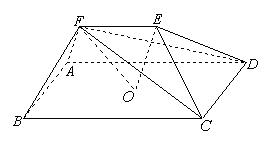
2、如图,在五面体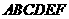 中,点
中,点 是矩形
是矩形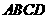 的对角线的交点,面
的对角线的交点,面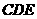 是等边三角形,棱
是等边三角形,棱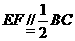 .
.
 (1)证明
(1)证明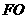 //平面
//平面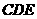 ;(线面平行时用)
;(线面平行时用)
(2)设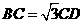 ,证明
,证明 平面
平面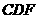 .(线面垂直时用)
.(线面垂直时用)
1、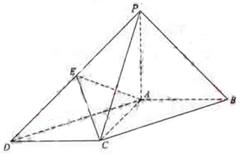 (将线面平行转变为线线平行):如图,在底面为平行四边形的四棱锥
(将线面平行转变为线线平行):如图,在底面为平行四边形的四棱锥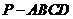 中,
中,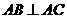 ,
,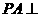 平面
平面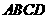 ,且
,且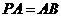 ,点
,点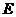 是
是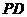 的中点.
的中点.
(Ⅱ)求证: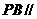 平面
平面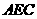 ;
;
(6)
3、三垂线定理及逆定理
在平面内的一条直线,如果和这个平面内的一条斜线在这个平面内的射影垂直,那么它也和这条斜线垂直。
逆定理:在平面内的一条直线和这个平面内的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直。
其主要作用有:①证明问题:如线线、线面、面面垂直的证明;
例 题
2、直线与平面所成的角
一条直线若是平面的斜线,那么它和它在平面上的射影所成的锐角,叫做这条直线与平面所成的角。特别地,若这条直线是平面的垂线,那么这条直线与平面所成的角是直角;如果这条直线平行于这个平面,那么直线与平面所成的角是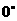 。
。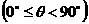
结论:斜线与平面所成的角,是这条直线和平面内经过斜足的直线所成的一切角中最小的角。
1、斜线长定理--从平面外一点所引的垂线段和斜线段中
①射影相等的两条斜线段相等,射影较长的斜线段也较长;
②相等的两条斜线段的射影相等,较长的斜线段的射影也较长;
③垂线段比任何一条斜线段都短
三)平行的性质:
(1) 定义:两个平行平面没有公共点.(常用于反证)
(2) 性质定理一:若一个平面与两个平行平面都相交,则两交线平行.(面面平行得线线平行,用于判定两直线平行)
(3) 性质定理二:两个平行平面中的一个平面内的所有直线平行于另一个平面.(面面平行得线面平行,用于判定线面平行)
(4) 一条直线垂直于两个平行平面中的一个平面,必垂直于另一个平面.(用来判定直线与平面垂直)
一般地,一条直线与两个平行平面所成的角相等,但反之不然.
(5) 夹在两个平行平面间的平行线段相等.特别地,两个平行平面间的距离处处相等.
二)平行的判定:
(1)定义:没有公共点的两个平面平行.(常用于反证)
(2)判定定理:若一个平面内的两条相交直线平行于另一平面,则这两个平面平行.(线面平行得面面平行)
(3)垂直于同一条直线的两个平面平行.
(4)平行于同一个平面的两个平面平行.
(5)过已知平面外一点作这个平面的平行平面有且只有一个.
一)位置关系:平行:没有公共点.
相交:至少有一个公共点,必有一条公共直线,公共点都在公共直线上.
相交包括垂直相交和斜交.
知识点:
15.已知f(x+1)=3x+4,则f-1(x+1)=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com