
题目列表(包括答案和解析)
11.(2010广东理数)已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=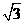 , A+C=2B,则sinC= .
, A+C=2B,则sinC= .
3. (2010江苏卷)8、函数y=x2(x>0)的图像在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k为正整数,a1=16,则a1+a3+a5=____▲_____
[解析]考查函数的切线方程、数列的通项。
在点(ak,ak2)处的切线方程为: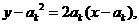 当
当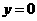 时,解得
时,解得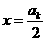 ,
,
所以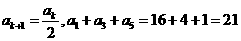 。
。
11.(2010福建理数)在等比数列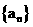 中,若公比
中,若公比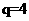 ,且前3项之和等于21,则该数列的通项公式
,且前3项之和等于21,则该数列的通项公式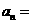 .
.
[答案]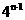
[解析]由题意知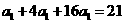 ,解得
,解得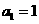 ,所以通项
,所以通项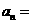
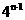 。
。
[命题意图]本题考查等比数列的通项公式与前n项和公式的应用,属基础题。
15.(2010湖南理数)若数列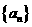 满足:对任意的
满足:对任意的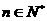 ,只有有限个正整数
,只有有限个正整数 使得
使得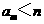 成立,记这样的
成立,记这样的 的个数为
的个数为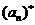 ,则得到一个新数列
,则得到一个新数列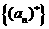 .例如,若数列
.例如,若数列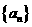 是
是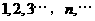 ,则数列
,则数列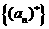 是
是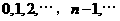 .已知对任意的
.已知对任意的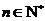 ,
,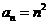 ,则
,则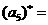 ,
,
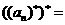
 .
.

11.(2010陕西文数)观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=
(1+2+3+4)2,…,根据上述规律,第四个等式为13+23+33+43+53=(1+2+3+4+5)2(或152).
解析:第i个等式左边为1到i+1的立方和,右边为1到i+1和的完全平方
所以第四个等式为13+23+33+43+53=(1+2+3+4+5)2(或152).
(2010辽宁文数)(14)设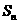 为等差数列
为等差数列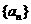 的前
的前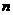 项和,若
项和,若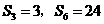 ,则
,则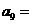 。
。
解析:填15. 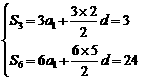 ,解得
,解得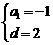 ,
,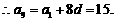 K^S*5U.C#
K^S*5U.C#
(2010辽宁理数)(16)已知数列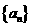 满足
满足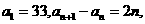 则
则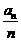 的最小值为__________.
的最小值为__________.
[答案]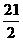
[命题立意]本题考查了递推数列的通项公式的求解以及构造函数利用导数判断函数单调性,考查了同学们综合运用知识解决问题的能力。
[解析]an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2[1+2+…(n-1)]+33=33+n2-n
所以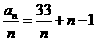
设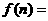
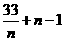 ,令
,令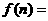
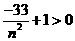 ,则
,则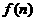 在
在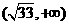 上是单调递增,在
上是单调递增,在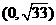 上是递减的,因为n∈N+,所以当n=5或6时
上是递减的,因为n∈N+,所以当n=5或6时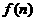 有最小值。
有最小值。
又因为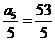 ,
,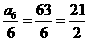 ,所以,
,所以,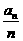 的最小值为
的最小值为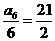
(2010浙江文数)(14)在如下数表中,已知每行、每列中的树都成等差数列,
那么,位于下表中的第n行第n+1列的数是 。

答案: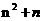
(2010天津文数)(15)设{an}是等比数列,公比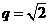 ,Sn为{an}的前n项和。记
,Sn为{an}的前n项和。记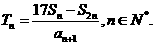 设
设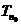 为数列{
为数列{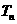 }的最大项,则
}的最大项,则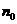 =
。
=
。
[答案]4
[解析]本题主要考查了等比数列的前n项和公式与通项及平均值不等式的应用,属于中等题。
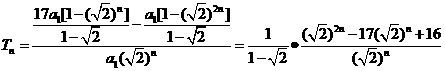
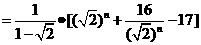 因为
因为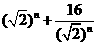 ≧8,当且仅当
≧8,当且仅当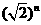 =4,即n=4时取等号,所以当n0=4时Tn有最大值。
=4,即n=4时取等号,所以当n0=4时Tn有最大值。
[温馨提示]本题的实质是求Tn取得最大值时的n值,求解时为便于运算可以对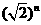 进行换元,分子、分母都有变量的情况下通常可以采用分离变量的方法求解.
进行换元,分子、分母都有变量的情况下通常可以采用分离变量的方法求解.
15.[答案]CD DE
[解析]在Rt△ADB中DC为高,则由射影定理可得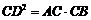 ,故
,故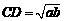 ,即CD长度为a,b的几何平均数,将OC=
,即CD长度为a,b的几何平均数,将OC=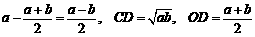 代入
代入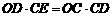 可得
可得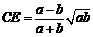 故
故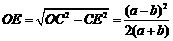 ,所以ED=OD-OE=
,所以ED=OD-OE=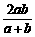 ,故DE的长度为a,b的调和平均数.
,故DE的长度为a,b的调和平均数.
19.(2010广东文数)(本题满分12分)
某营养师要求为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营状中至少含64个单位的碳水化合物和42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
 解:设为该儿童分别预订
解:设为该儿童分别预订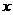 个单位的午餐和
个单位的午餐和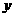 个单位的晚餐,设费用为F,则F
个单位的晚餐,设费用为F,则F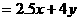 ,由题意知:
,由题意知:
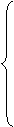
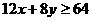
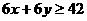
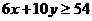
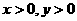
画出可行域:
变换目标函数: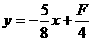

(2010湖北理数)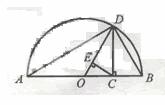 15.设a>0,b>0,称
15.设a>0,b>0,称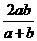 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
19.(2010广东理数)(本小题满分12分)
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素C;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素C.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
解:设该儿童分别预订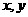 个单位的午餐和晚餐,共花费
个单位的午餐和晚餐,共花费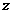 元,则
元,则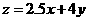 。
。
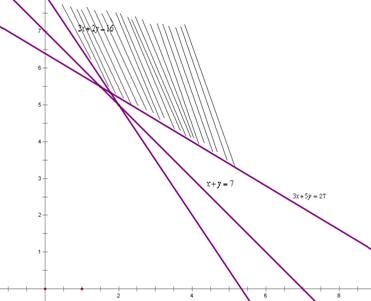 可行域为
可行域为
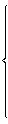 12
x+8 y ≥64
12
x+8 y ≥64
6 x+6 y ≥42
6 x+10 y ≥54
x≥0, x∈N
y≥0, y∈N
即
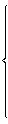 3
x+2 y ≥16
3
x+2 y ≥16
x+ y ≥7
3 x+5 y ≥27
x≥0, x∈N
y≥0, y∈N
作出可行域如图所示:
经试验发现,当x=4,y=3 时,花费最少,为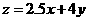 =2.5×4+4×3=22元.[来源:KS
=2.5×4+4×3=22元.[来源:KS
17.(2010湖南文数) (本小题满分12分)
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
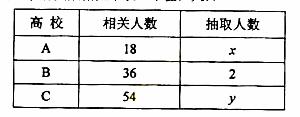
(I) 求x,y ;
(II) 若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。


(2010全国卷2理数)(20)(本小题满分12分)
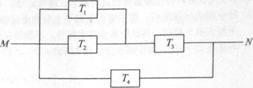
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(Ⅰ)求p;
(Ⅱ)求电流能在M与N之间通过的概率;
(Ⅲ)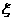 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求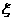 的期望.
的期望.
[命题意图]本试题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及数学期望,考查分类讨论的思想方法及考生分析问题、解决问题的能力.
4.(2010福建理数)函数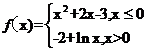 的零点个数为 ( )
的零点个数为 ( )
A.0 B.1 C.2 D.3
[答案]C
[解析]当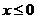 时,令
时,令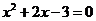 解得
解得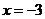 ;
;
当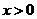 时,令
时,令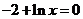 解得
解得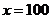 ,所以已知函数有两个零点,选C。
,所以已知函数有两个零点,选C。
[命题意图]本题考查分段函数零点的求法,考查了分类讨论的数学思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com