
题目列表(包括答案和解析)
5.(2010广东理数) “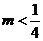 ”是“一元二次方程
”是“一元二次方程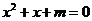 ”有实数解的
”有实数解的
A.充分非必要条件 B.充分必要条件
C.必要非充分条件 D.非充分必要条件
2.(2010江西理数)若集合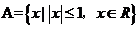 ,
,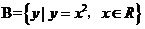 ,则
,则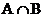 =( )
=( )
A. 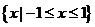 B.
B.
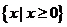
C. 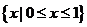 D.
D. 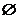
[答案] C
[解析]考查集合的性质与交集以及绝对值不等式运算。常见的解法为计算出集合A、B;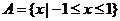 ,
,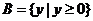 ,解得
,解得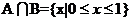 。在应试中可采用特值检验完成。
。在应试中可采用特值检验完成。
(2010安徽文数)(1)若A=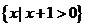 ,B=
,B=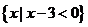 ,则
,则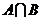 =
=
(A)(-1,+∞) (B)(-∞,3) (C)(-1,3) (D)(1,3)
C
[解析]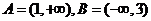 ,
,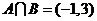 ,故选C.
,故选C.
[方法总结]先求集合A、B,然后求交集,可以直接得结论,也可以借助数轴得交集.
(2010浙江文数)(6)设0<x<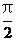 ,则“x sin2x<1”是“x sinx<1”的
,则“x sin2x<1”是“x sinx<1”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
解析:因为0<x<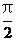 ,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
,所以sinx<1,故xsin2x<xsinx,结合xsin2x与xsinx的取值范围相同,可知答案选B,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题
(2010浙江文数)(1)设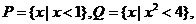 则
则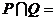
(A)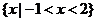 (B)
(B)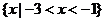
(C)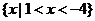 (D)
(D)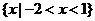
解析: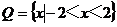 ,故答案选D,本题主要考察了集合的基本运算,属容易题
,故答案选D,本题主要考察了集合的基本运算,属容易题
(2010山东文数)(7)设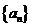 是首项大于零的等比数列,则“
是首项大于零的等比数列,则“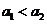 ”是“数列
”是“数列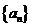 是递增数列”的
是递增数列”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
答案:C
(2010山东文数)(1)已知全集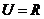 ,集合
,集合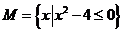 ,则
,则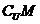 =
=
A. 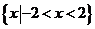 B.
B. 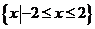
C.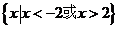 D.
D. 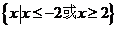
答案:C
(2010北京文数)⑴ 集合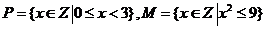 ,则
,则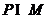 =
=
(A) {1,2} (B) {0,1,2} (C){1,2,3} (D){0,1,2,3}
答案:B
(2010北京理数)(6)a、b为非零向量。“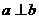 ”是“函数
”是“函数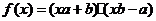 为一次函数”的
为一次函数”的
(A)充分而不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
答案:B
(2010北京理数)(1) 集合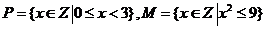 ,则
,则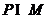 =
=
(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x≤3}
答案:B
(2010天津文数)(7)设集合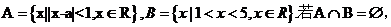 则实数a的取值范围是
则实数a的取值范围是
(A)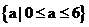 (B)
(B)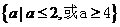
(C)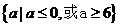 (D)
(D)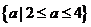
[答案]C
[解析]本题主要考查绝对值不等式的基本解法与集合交集的运算,属于中等题。
由|x-a|<1得-1<x-a<1,即a-1<x<a+1.如图 由图可知a+1≦1或a-1≧5,所以a≦0或a≧6.
由图可知a+1≦1或a-1≧5,所以a≦0或a≧6.
[温馨提示]不等式型集合的交、并集通常可以利用数轴进行,解题时注意验证区间端点是否符合题意。
(2010天津理数)(9)设集合A=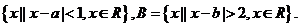 若A
若A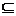 B,则实数a,b必满足
B,则实数a,b必满足
(A)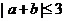 (B)
(B)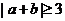
(C)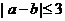 (D)
(D)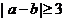
[答案]D
[解析]本题主要考查绝对值不等式的解法与几何与结合之间的关系,属于中等题。
A={x|a-1<x<a+1},B={x|x<b-2或x>b+2}
因为A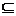 B,所以a+1
B,所以a+1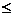 b-2或a-1
b-2或a-1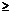 b+2,即a-b
b+2,即a-b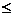 -3或a-b
-3或a-b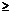 3,即|a-b|
3,即|a-b|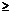 3
3
[温馨提示]处理几何之间的子集、交、并运算时一般利用数轴求解。
1.(2010辽宁理数)已知A,B均为集合U={1,3,5,7,9}的子集,且A∩B={3},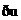 B∩A={9},则A=
B∩A={9},则A=
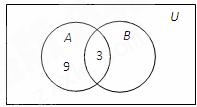 (A){1,3} (B){3,7,9} (C){3,5,9} (D){3,9}
(A){1,3} (B){3,7,9} (C){3,5,9} (D){3,9}
[答案]D
[命题立意]本题考查了集合之间的关系、集合的交集、补集的运算,考查了同学们借助于Venn图解决集合问题的能力。
[解析]因为A∩B={3},所以3∈A,又因为
 B∩A={9},所以9∈A,所以选D。本题也可以用Venn图的方法帮助理解。
B∩A={9},所以9∈A,所以选D。本题也可以用Venn图的方法帮助理解。
(2010全国卷2文数)
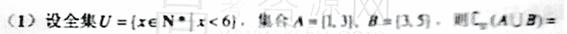
(A)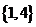 (B)
(B)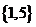 (C)
(C)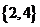 (D)
(D)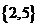
[解析] C :本题考查了集合的基本运算. 属于基础知识、基本运算的考查.
∵
A={1,3}。B={3,5},∴ 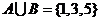 ,∴
,∴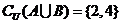 故选 C .
故选 C .
1.(2010陕西文数)集合A={x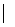 -1≤x≤2},B={x
-1≤x≤2},B={x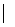 x<1},则A∩B= [D]
x<1},则A∩B= [D]
(A){x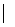 x<1} (B){x
x<1} (B){x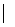 -1≤x≤2}
-1≤x≤2}
(C) {x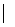 -1≤x≤1}
(D) {x
-1≤x≤1}
(D) {x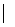 -1≤x<1}
-1≤x<1}
解析:本题考查集合的基本运算
由交集定义得{x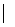 -1≤x≤2}∩{x
-1≤x≤2}∩{x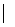 x<1}={x
x<1}={x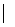 -1≤x<1}
-1≤x<1}
(2010辽宁文数)(1)已知集合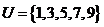 ,
,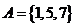 ,则
,则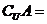
(A)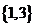 (B)
(B)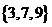 (C)
(C)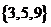 (D)
(D)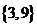
解析:选D.
在集合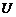 中,去掉
中,去掉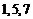 ,剩下的元素构成
,剩下的元素构成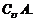
(2010辽宁理数)(11)已知a>0,则x0满足关于x的方程ax=6的充要条件是
(A)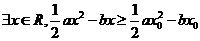 (B)
(B) 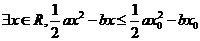
(C) 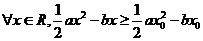 (D)
(D) 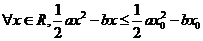
[答案]C
[命题立意]本题考查了二次函数的性质、全称量词与充要条件知识,考查了学生构造二次函数解决问题的能力。
[解析]由于a>0,令函数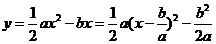 ,此时函数对应的开口向上,当x=
,此时函数对应的开口向上,当x=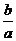 时,取得最小值
时,取得最小值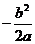 ,而x0满足关于x的方程ax=b,那么x0==
,而x0满足关于x的方程ax=b,那么x0==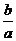 ,ymin=
,ymin=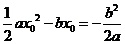 ,那么对于任意的x∈R,都有
,那么对于任意的x∈R,都有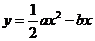 ≥
≥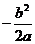 =
=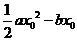
6.(2010陕西文数)“a>0”是“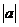 >0”的 [A]
>0”的 [A]
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解析:本题考查充要条件的判断
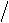
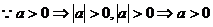 ,
,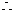 a>0”是“
a>0”是“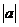 >0”的充分不必要条件
>0”的充分不必要条件
2.(2010湖南文数) 下列命题中的假命题是
A. 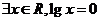 B.
B. 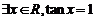
C. 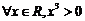 D.
D.
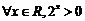
[答案]C
[解析]对于C选项x=1时,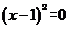 ,故选C
,故选C
(2010浙江理数)(1)设P={x︱x<4},Q={x︱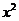 <4},则
<4},则
(A)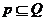 (B)
(B)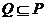 (C)
(C)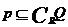 (D)
(D)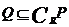
解析: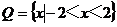 ,可知B正确,本题主要考察了集合的基
,可知B正确,本题主要考察了集合的基
本运算,属容易题
16.(2010上海文数)“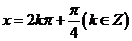 ”是“
”是“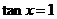 ”成立的
[答]( )
”成立的
[答]( )
(A)充分不必要条件. (B)必要不充分条件.
(C)充分条件. (D)既不充分也不必要条件.
解析: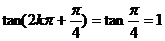 ,所以充分;但反之不成立,如
,所以充分;但反之不成立,如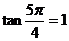
1.[答案]D
[解析]观察图形可知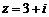 ,则
,则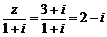 ,即对应点H(2,-1),故D正确.
,即对应点H(2,-1),故D正确.
2、(2010江苏卷)设复数z满足z(2-3i)=6+4i(其中i为虚数单位),则z的模为______▲_____.
[解析] 考查复数运算、模的性质。z(2-3i)=2(3+2 i), 2-3i与3+2 i的模相等,z的模为2。
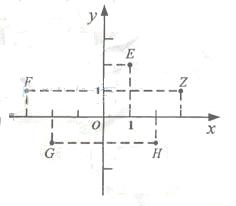 (2010湖北理数)1.若i为虚数单位,图中复平面内点Z表示复数Z,则表示复数
(2010湖北理数)1.若i为虚数单位,图中复平面内点Z表示复数Z,则表示复数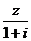 的点是
的点是
A.E B.F C.G D.H
4.(2010上海文数)若复数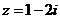 (
(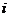 为虚数单位),则
为虚数单位),则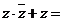
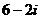 。
。
解析:考查复数基本运算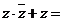
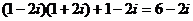
(2010重庆理数)(11)已知复数z=1+I ,则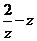 =____________.
=____________.
解析: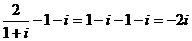
(2010北京理数)(9)在复平面内,复数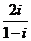 对应的点的坐标为
。
对应的点的坐标为
。
答案:(-1,1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com