
题目列表(包括答案和解析)
6.设数列{an}的前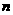 项和为Sn.已知a1=a,an+1=Sn+3n,n∈N*.(1)设bn=Sn-3n,求数列{bn}的通项公式;(2)若an+1≥an,n∈N*,求a的取值范围.
项和为Sn.已知a1=a,an+1=Sn+3n,n∈N*.(1)设bn=Sn-3n,求数列{bn}的通项公式;(2)若an+1≥an,n∈N*,求a的取值范围.
5.已知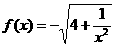 数列
数列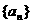 的前n项和为
的前n项和为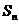 ,点
,点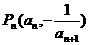 在曲线
在曲线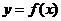 上
上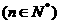 且
且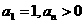 .
.
(1)求数列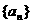 的通项公式;
的通项公式;
(2)数列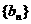 的前n项和为且
的前n项和为且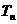 满足
满足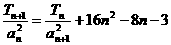 ,设定
,设定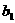 的值使得数列
的值使得数列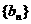 是等差数列;
是等差数列;
(3)求证: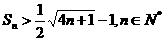 .
.
4.设数列{an}的各项都是正数,且对任意n∈N+,都有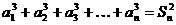 ,记Sn为数列{an}的前n项和.
,记Sn为数列{an}的前n项和.
(1)求数列{an}的通项公式;
(2)若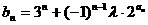 (
(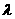 为非零常数,n∈N+),问是否存在整数
为非零常数,n∈N+),问是否存在整数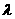 ,使得对任意 n∈N+,都有bn+1>bn.
,使得对任意 n∈N+,都有bn+1>bn.
3.在直角坐标平面上有一点列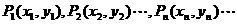 ,对一切正整数
,对一切正整数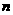 ,点
,点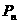 位于函数
位于函数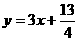 的图象上,且
的图象上,且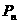 的横坐标构成以
的横坐标构成以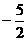 为首项,
为首项,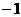 为公差的等差数列
为公差的等差数列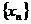 .
.
⑴求点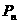 的坐标;
的坐标;
⑵设抛物线列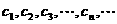 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于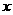 轴,第
轴,第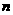 条抛物线
条抛物线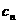 的顶点为
的顶点为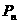 ,且过点
,且过点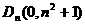 ,记与抛物线
,记与抛物线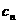 相切于
相切于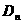 的直线的斜率为
的直线的斜率为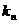 ,求:
,求: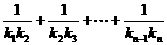 .
.
⑶设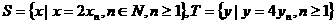 ,等差数列
,等差数列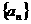 的任一项
的任一项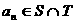 ,其中
,其中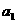 是
是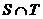 中的最大数,
中的最大数,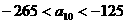 ,求
,求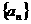 的通项公式.
的通项公式.
2.已知数列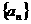 中,
中,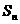 是其前
是其前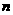 项和,并且
项和,并且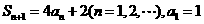 ,
,
⑴设数列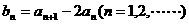 ,求证:数列
,求证:数列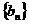 是等比数列;
是等比数列;
⑵设数列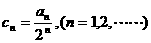 ,求证:数列
,求证:数列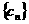 是等差数列;
是等差数列;
⑶求数列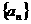 的通项公式及前
的通项公式及前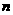 项和.
项和.
1.已知数列{a }是公差d≠0的等差数列,其前n项和为S
}是公差d≠0的等差数列,其前n项和为S .
.
(1)求证:点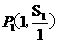 ,
,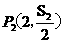 ……
……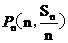 在同一条直线l1上;
在同一条直线l1上;
(2)过点Q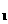 (1,a
(1,a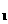 ),Q
),Q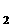 (2,a
(2,a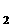 )作直线12,设l
)作直线12,设l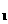 与l
与l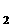 的夹角为θ,
的夹角为θ,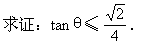
17 已知函数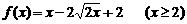
(Ⅰ)求反函数;
(Ⅱ)若数列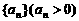 的前n项和
的前n项和 求数列
求数列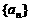 的通项公式;
的通项公式;
(Ⅲ)[理]令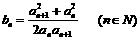 ,求
,求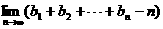
18 已知 、
、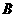 是
是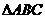 的两个内角,且
的两个内角,且 、
、 是方程
是方程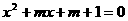 的两个实根,求
的两个实根,求 的取值范围
的取值范围
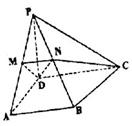 19 在四棱锥
19 在四棱锥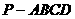 中,
中,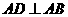 ,
,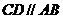 ,
,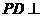 底面
底面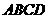 ,
, 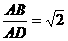 ,直线
,直线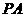 与底面
与底面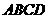 成
成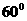 角,点
角,点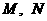 分别是
分别是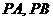 的中点
的中点
(1)求二面角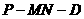 的大小;
的大小;
(2)当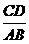 的值为多少时,
的值为多少时,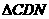 为直角三角形
为直角三角形
20 投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过
多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋
(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率
(Ⅱ)[文]求该人两次投掷后得2分的概率
[理]求该人两次投掷后得分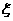 的数学期望
的数学期望
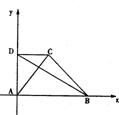
21 如图,直角梯形ABCD中,AB//CD,AB⊥AD,对角线AC⊥BD,且A(0,0),B(4,0)
(1)求点C的轨迹M;
 (2)过点B的直线
(2)过点B的直线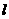 交轨迹M于E,F两点,求证:AE
交轨迹M于E,F两点,求证:AE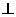 AF
AF
22 已知函数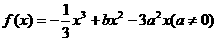 在
在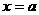 处取得极值,
处取得极值,
(1)用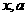 表示
表示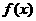 ;
;
(2)设函数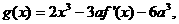 如果
如果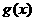 在区间(0,1)上存在极小值,求实数
在区间(0,1)上存在极小值,求实数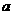 的取值范围
的取值范围
13 已知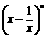 的展开式中所有二项式系数的和为512,则展开式中
的展开式中所有二项式系数的和为512,则展开式中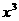 项的系数为_ ____
项的系数为_ ____
 14 已知函数
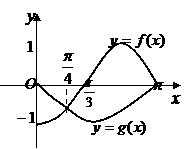
14 已知函数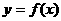 是偶函数,
是偶函数,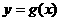 是奇函数,
是奇函数,
它们的定义域是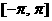 ,且它们在
,且它们在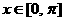 上的
上的
图象如图所示,则不等式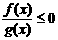 的解集
的解集
是
15 已知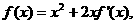 则
则
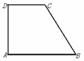 16 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角
16 已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角
梯形ABCD,如图AD⊥AB,AD⊥DC,AB=2,BC=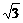 ,CD=1,则这
,CD=1,则这
个三棱锥外接球的表面积是__________(结果可含π)
1 已知命题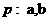 是整数;命题
是整数;命题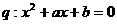 有且仅有整数解,则
有且仅有整数解,则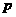 是
是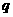 的( )
的( )
A 充分不必要条件;B 必要非充分条件; C 充要条件;D 不充分也不必要条件
2 若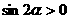 且
且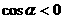 ,则
,则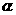 是 ( )
是 ( )
A 第二象限角 B 第一或第三象限角
C 第三象限角 D 第二或第四象限角
3 设等差数列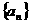 的公差为2,前
的公差为2,前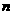 项和为
项和为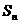 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A 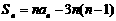 B
B 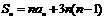
C 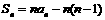 D
D 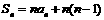
4 [理]设函数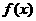 在
在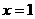 处连续,且
处连续,且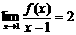 ,则
,则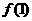 等于( )
等于( )
A 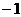 B
B  C
C 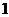 D
D 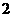
[文]不等式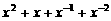 <0的解集 ( )
<0的解集 ( )
A 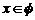 B
B 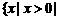 C
C 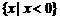 D
D 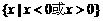
5 如果f(a+b)=f(a)•f(b)且f(1)=2,则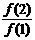 +
+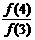 +
+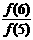 +…+
+…+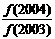 等于( )
等于( )
A 2003 B 1001 C 2004 D 2002
6 若一个圆的圆心在抛物线y2=4x的焦点处,且此圆与直线x+y+1=0相切,则这个圆的方程是( )
A x2+y2-2x-1=0 B x2+y2+2x+1=0
C x2+y2-2y+1=0 D x2+y2+2y+1=0
7 已知x、y满足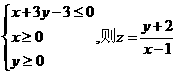 的取值范围是 ( )
的取值范围是 ( )
A [-2,1] B 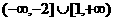
C [-1,2] D 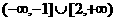
8 已知单位正方体ABCD-A1B1C1D1的对棱BB1、DD1上有两个动点E、F,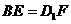
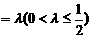 设EF与AB所成的角为a,与BC所成的角为b,则a+b的最小值( )
设EF与AB所成的角为a,与BC所成的角为b,则a+b的最小值( )
A 不存在 B 等于60° C 等于90° D 等于120°
9 某城市对一种售价为每件160元的电子产品征收附加税,税率为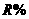 (即每销售100元征税
(即每销售100元征税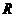 元),若年销售量为30-
元),若年销售量为30-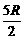 万件,要使附加税不少于128万元,则R的取值范围是( )
万件,要使附加税不少于128万元,则R的取值范围是( )
A [4,8] B [6,10] C [4%,8%] D [6%,10%]
10 以抛物线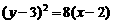 上任意一点P为圆心作圆与y轴相切,则这些圆必过定点
上任意一点P为圆心作圆与y轴相切,则这些圆必过定点
A (3,3) B (4,3) C (2,3) D (3,0)
11 在正四面体的一个顶点处,有一只蚂蚁每一次都以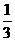 的概率从一个顶点爬到另一个顶点 那么它爬行了4次又回到起点的概率是 ( )
的概率从一个顶点爬到另一个顶点 那么它爬行了4次又回到起点的概率是 ( )
A 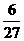 B
B 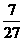 C
C 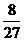 D
D 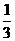
12 某段街道旁边规划树立10块广告牌,广告底色选用红、绿两种颜色,则相邻两块广告底色不同为绿色的配色方案的种数为 ( )
A 72 B 78 C 144 D 156
13 已知有公共端点的向量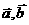 不共线,|
不共线,| |=1,|
|=1,|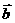 |=2 则与向量
|=2 则与向量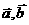 的夹角平分线平行的单位向量是______________
的夹角平分线平行的单位向量是______________
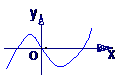 14 函数f(x)=ax3+bx2+cx+d的图象(如图),则实数a b c d与零的
14 函数f(x)=ax3+bx2+cx+d的图象(如图),则实数a b c d与零的
大小关系是__________;方程f(x)=f’(x)实根的个数_____________
15 设命题p: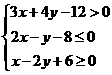 (x y∈R),命题q:x2+y2
(x y∈R),命题q:x2+y2 r2(x、y、
r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为__________
r2(x、y、
r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为__________
16 删去正整数列中的所有奇数的完全平方数,得到一个新数列,此新数列的第2004项是____
三 解答题:(本大题6小题,共74分,必需写出必要的文字说明 推理过程或计算步骤 )
17 (本题满分12分)
同时抛掷15枚均匀的硬币一次 (1)试求至多有1枚正面向上的概率;(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由
18 (本题满分12分)
已知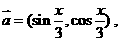
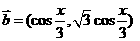 ,函数
,函数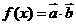
(1)将f(x)写成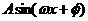 的形式,并求其图象对称中心的坐标;
的形式,并求其图象对称中心的坐标;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域
19 (本题满分12分)
已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足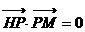 ,
,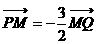 (1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S R,求证:抛物线S R两点处的切线的交点B恒在一条直线上
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S R,求证:抛物线S R两点处的切线的交点B恒在一条直线上
20 (本题满分12分)
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=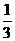 GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为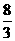
(1)求异面直线GE与PC所成的角;
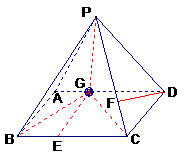 (2)求点D到平面PBG的距离;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求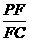 的值
的值
21 (本题满分12分)
在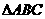 中,已知
中,已知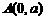 ,
,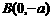 ,
,
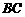 两边所在的直线分别与
两边所在的直线分别与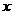 轴交于原点同侧的点
轴交于原点同侧的点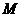
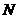 ,且满足
,且满足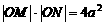 (
(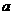 为不等于零的常数)
为不等于零的常数)
(1)求点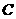 的轨迹方程;
的轨迹方程;
(2)如果存在直线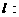
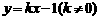 ,使
,使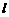 与点
与点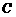 的轨迹相交于不同的
的轨迹相交于不同的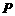
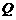 两点,且
两点,且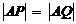 ,求
,求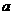 的取值范围
的取值范围
22 (本题满分14分)
设数列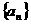 满足:若
满足:若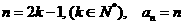 ;若
;若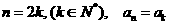
(1)求: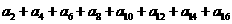 ;
;
(2)若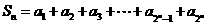 ,求证:
,求证: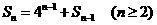 ;
;
(3)证明: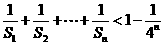
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com