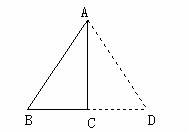
10.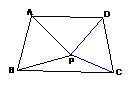如图所示，△ABP和△CPD是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠1＝15°， ②AD∥BC，③直线PC⊥AB，④四边形ABCD是轴对称图形。其中正确的结论的个数是(　　)

A、1　　B、2　　　C、3　　　D、4

第Ⅱ卷(非选择题　 共90分)

7.下列说法中，正确的个数有(　 )

(1)有一个外角是120°的等腰三角形是等边三角形；(2)有两个外角相等的等腰三角形是等边三角形；(3)三个外角都相等的三角形是等边三角形；(4) △ABC中三边为a、b、c，满足关系式(a－b)(b－c)(c－a)＝0，则这个三角形是等边三角形。

A、1个　　 B、2个　　 C、3个　　 D、4个

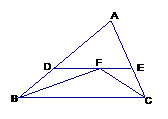＃8.如图，△ABC中，已知∠ABC和∠ACB的角平分线相交于F，经过F作DE∥BC，交AB于点D，交AC于点E，若BD+CE=9，则线段DE的长为(　　 )

A、9　　　 B、8　　　　 C、7　　　　 D、6

＃9.如图，已知等边△ABC中，BD＝CE，AD与BE交于P，则∠APE的度数是(　)

A、45°　　　B、55°　　C、60°　　　D、75°

6.等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角为(　　 )

A、30°　　　 B、150°　　　 C、30°或150°　　　　 D、120°

5.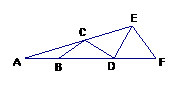如图，∠A=15°，AB=BC=CD=DE=EF，则∠EDF等于(　　 )

A、90°　　 B、75°　　　　 C、70°　　　　 D、60°

4.等腰三角形一腰上的高与底边所成的角等于(　 )

A、顶角　　 B、顶角的一半　　　 C、顶角的2倍　　　 D、底角的一半

2.等腰三角形底边长为6㎝，一腰上的中线把腰长分成两部分的差为2㎝，则腰长为(　　 )

A、4㎝　　　　 B、8㎝　　　　　 C、4㎝或8㎝　　　　 D、以上都不对

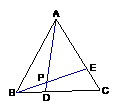
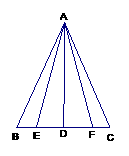＃3.如图，在△ABC中，AD是高，E、F在BC上，且BE=CF，则图中全等三角形有(　　 )

A、1对　　 B、2对　　　 C、3对　　　　 D、4对

1.等腰三角形的一边长为4cm,另一边长为9cm,则它的周长为(　　)

A、13cm　　 B、17cm　　 C、22cm　　　 D、17cm或22cm

9. 解：(1)图②-⑤ 中的关系依次是：

h₁+h₂+h₃=h； h₁-h₂+h₃=h； h₁+h₂+h₃=h； h₁+h₂-h₃=h．　　

(2)图②中，h₁+h₂+h₃=h．

证明：连结AP， 则S_ΔAPB+S_ΔAPC=S_ΔABC．　　

∴ ．　

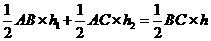又 h₃=0，AB=AC=BC， ∴ h₁+h₂+h₃==h．　

　 (3)证明：图④中，h₁+h₂+h₃=h．

过点P作RS∥BC与边AB、AC相交于R、S．

　　　　 在△ARS中，由图②中结论知：h₁+h₂+0=h-h₃．

∴ h₁+h₂+h₃=h．

说明：(2)与(3)问，通过作辅助线，利用证全等三角形的方法类似给分．

　 (4)h₁+h₃+h₄= ．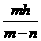 　

8.　 证明：延长BC到D，使CD=BC，连结AD．

　　 ∵∠ACB=90°，∴∠ACD=90°．

　　 又∵AC=AC，∴△ACB≌△ACD(SAS)．

　　 ∴AB=AD．∵CD=BC， ∴BC=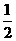BD． 又∵BC=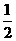AB，

　　 ∴AB=BD． ∴AB=AD=BD， 即△ABD为等边三角形．

　　 ∴∠B=60°．

　　 在Rt△ABC中，∠BAC=30°．

7. 解：在Rt△ABC中，∠CAB=30°，AB=10cm． ∴BC=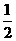AB=5cm．

　 ∵CB₁⊥AB， ∴∠B+∠BCB₁=90°． 又∵∠A+∠B=90°，∴∠BCB₁=∠A=30°．

　　 在Rt△ACB₁中，BB₁=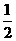BC=2.5cm． ∴AB₁=AB-BB₁=10-2.5=7.5(cm)．

　　 ∴在Rt△AB₁C₁中，∠A=30°．

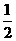　　 ∴B₁C₁=AB₁=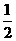×7.5=3.75(cm)．