
题目列表(包括答案和解析)
6、若等腰直角三角形的腰长为4,腰上的高为2,则此三角形的顶角为()
A、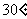 B、
B、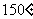 C、
C、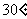 或
或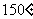 D、
D、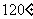
5、如图长方形ABCD中,AB=3,BC=4,将该矩形折叠,使点C与点A重合,则折痕EF的长为()
 A、3.74B3.75、C、3.76D、3.77
A、3.74B3.75、C、3.76D、3.77
4、CD是直角△ABC斜边AB上的高,若AB=1,AC:BC=4:1,则CD的长为()
A、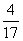 B、
B、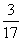 C、
C、 D、
D、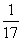
3、 直角三角形中,斜边长为5cm,周长为12cm,则它的面积为()
A、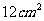 B、
B、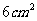 C、
C、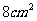 D、
D、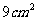
2、 直角三角形斜边的平方等于两直角边乘积的2倍,则这个直角三角形有一个锐角是()
A、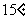 B、
B、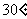 C、
C、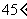 D、
D、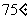
1、 在△ABC中,AB=AC=10,BD是AC边上的高,DC=2,则BD等于()
A、4 B、6 C、8 D、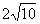
13.11勾股定理的应用练习(1)
第1题.  如图,△ABC中,∠ACB=90º,CD为AB边上的高,若∠A=30º,AB=16,则BC=______,BD=______,CD=______.
如图,△ABC中,∠ACB=90º,CD为AB边上的高,若∠A=30º,AB=16,则BC=______,BD=______,CD=______.
答案:8,4,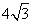 .
.
第2题. 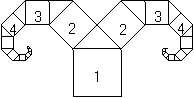 如图是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,以此类推,若正方形1的边长为64cm,则正方形7的边长为_________cm.
如图是一种“牛头形”图案,其作法是:从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2,以此类推,若正方形1的边长为64cm,则正方形7的边长为_________cm.
答案:8.
第3题. 甲、乙两人从同一地点出发,甲往东走了4km,乙往南走了3km,这时,甲、乙两人相距______.
答案:5km
第4题. 如果梯子底端离建筑物9m,那么15m长的梯子可达到建筑物的高度是______.
答案:12m
第5题. 如图,一扇宽为4米,高为3米的栅栏门,需要一根长______米的木条像图中那样固定.
答案:5
第6题. 一块土地的形状如图所示,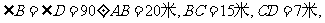 求这块土地的面积?
求这块土地的面积?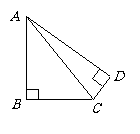
答案:234平方米
第7题. 某菜农修建一个塑料大棚(如图),若棚宽a=4m,高b=3m,长d=35m,求覆盖在顶上的塑料薄膜的面积.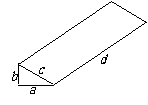
答案:175m2
第8题. 一游泳池长48cm,小方和小朱进行游泳比赛,从同一处出发,小方平均速度为3m/秒,小朱为3.1m/秒.但小朱一心想快,不看方向沿斜线游,而小方直游,俩人到达终点的位置相距14m.按各人的平均速度计算,谁先到达终点,为什么?
答案:小朱用16.13秒,小方用16秒,小方先到达终点
第9题. 如图,正方形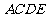 的面积为25cm,测量出
的面积为25cm,测量出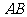 =12cm,
=12cm,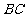 =13cm,问
=13cm,问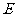 、
、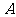 、
、 三点在一条直线上吗?为什么?
三点在一条直线上吗?为什么?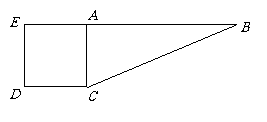
答案:在一条直线上,理由略
第10题. 从A到B有两种路线,一种走直线由A到B,另一种走折线,先从A直线到C,再由C直线到B,其中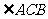 成直角,已知A到C为600m,C到B为800m,问从A到B走直线比走折线少走多少米?
成直角,已知A到C为600m,C到B为800m,问从A到B走直线比走折线少走多少米?
答案:400米
第11题. 如图,△ABC中,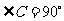 ,量出AC、BC的长,计算出AB(保留两个有效数字)
,量出AC、BC的长,计算出AB(保留两个有效数字)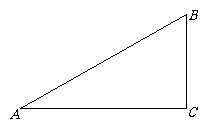
答案:略
第12题. 已知一个三角形的三边长分别是12cm,16cm,20cm,你能计算出这个三角形的面积吗?
答案:96平方厘米
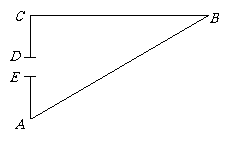
第13题. 某住宅小区的形状是如图所示的直角三角形,直角边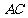 ,
,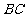 的长分别为600米、800米,
的长分别为600米、800米,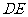 为小区的大门,大门宽5米,小区的周围用冬青围成了绿化带,问绿化带有多长?
为小区的大门,大门宽5米,小区的周围用冬青围成了绿化带,问绿化带有多长?
答案:2395米
第14题. 一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,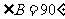 ,木板的面积为( )
,木板的面积为( )
A.60 B.30 C.24 D.12
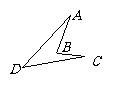
答案:C
第15题. 一个正方形的面积为1,那么以它的对角线为边长的正方形的面积是______.
答案:2
第16题. 如果一个直角三角形的斜边长为2m,有一条直角边为m.那么这个三角形的另一条直角边是多少?
答案: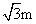
第17题. 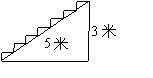 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?
如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?
答案:7米
第18题. 这是一个古代问题:有25尺长的梯子放置在一建筑物的垂直墙上,梯足距建筑物的底端7尺,若梯子的顶端滑下4尺,求梯足将滑走多少尺? 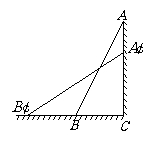
答案:由题意及勾股定理可知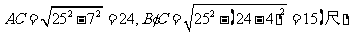 所以梯足滑走
所以梯足滑走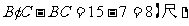
第19题. 如图,已知Rt△ABC中,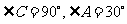 请你用刻度尺测量一下:AB为多长?BC为多长?你能发现二者长度的关系吗?再任画一个Rt△,且使一个锐角为
请你用刻度尺测量一下:AB为多长?BC为多长?你能发现二者长度的关系吗?再任画一个Rt△,且使一个锐角为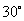 ,看一看
,看一看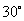 角所对的直角边与斜边的关系是什么规律.
角所对的直角边与斜边的关系是什么规律.

答案:可以发现,在Rt△ABC中,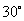 角所对的直角边等于斜边的一半
角所对的直角边等于斜边的一半
第20题. 已知线段a,求作线段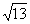 a时,可分别以2a和
___为直角边作直角三角形,斜边即为所求.
a时,可分别以2a和
___为直角边作直角三角形,斜边即为所求.
答案:3a
第21题. 等边三角形边长为2,则面积为________.
答案: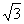
第22题. 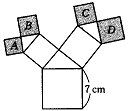 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是_______cm2.
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是_______cm2.
答案:49.
第23题. 如图是边长为1的8个小正方形组成的图形,请重新剪拼成一个正方形(画出裁剪线和重新拼成的图形).
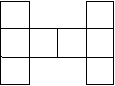 答案:
答案:

第24题. 小丽和小芳二人同时从公园去图书馆,都是每分钟走50米,小丽走直线用了10分钟,小芳先去家拿了钱去图书馆,小芳到家用了6分,从家到图书馆用了8分,小芳从公园到图书馆拐了个( )角.
A.锐角 B.直角 C.钝角 D.不能确定
 答案:B
答案:B
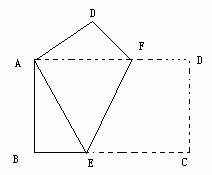
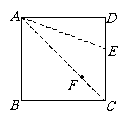
第25题. 已知:将正方形纸片ABCD折叠两次,第一次折痕为AC,第二次折痕为AE,且点D落在F处.若正方形边长为1,求DE.(见图)
答案: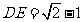
第26题. 如图所示,一块四边形的土地需要开发,测量有关数据为: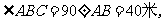
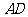 =130米,
=130米,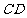 =120米,
=120米,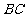 =30米,请你计算这块土地的面积.
=30米,请你计算这块土地的面积.
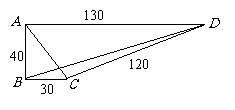
答案:3600平方米
第27题. 如图,要从电线杆离地面5m处向地面拉一条长7m的电缆,求地面电缆固定点A到电线杆底部B的距离.
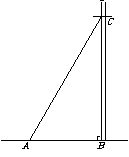
答案: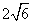
第28题. 如图,已知长方体的底边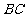 =12cm,
=12cm,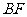 =9cm,长方体的高
=9cm,长方体的高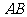 =8cm,求长方体的对角线
=8cm,求长方体的对角线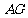 的长.
的长.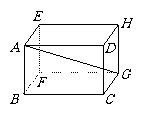
答案:17cm
第29题. 如图,一扇长方形大门,高3m,宽4m,为了加固大门,在大门的四边及对角线位置分别订上铁条, 问至少需要多长的铁条?
问至少需要多长的铁条?
答案:24米
第30题. 一艘轮船以20海里/时的速度离开港口向东北方向航行,另一艘轮船同时离开此港以22海里/时的速度向东南方向航行,2小时后两船相距多少海里?
答案: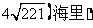
13.11-13.12勾股定理练习
第1题.  如图,四边形
如图,四边形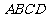 是正方形,
是正方形,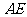 垂直于
垂直于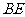 ,且
,且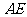 =3,
=3,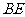 =4,阴影部分的面积是______.
=4,阴影部分的面积是______.
答案:19
第2题. 满足______的三个正整数,称为勾股数.
答案: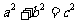
第3题. 在直角三角形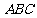 中,
中,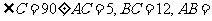 ______.
______.
答案:13
第4题. 在直角三角形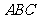 中,斜边
中,斜边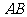 =2,则
=2,则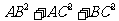 =______.
=______.
答案:8
第5题. 在长方形ABCD中,若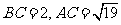 ,求AB.
,求AB.
答案:
第6题. 直角三角形的斜边长为10cm,且它的一条直角边是另一条直角边的3倍,试求它的面积.
答案:15cm2
第7题. 等腰三角形的面积为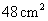 ,底边上的高为6cm,腰长为______.
,底边上的高为6cm,腰长为______.
答案:10cm
第8题. 如果直角三角形的一条直角边长为40,斜边长为41,那么另一条直角边的长为______.
答案:9
第9题. 如图,已知直角三角形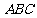 的两直角边
的两直角边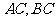 的长分别为4cm,3cm,求斜边
的长分别为4cm,3cm,求斜边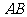 上的高
上的高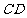 的长.
的长.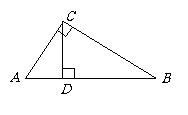
答案:2.4cm
第10题. 在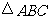 中,AB=AC,AD为BC边上的中线,如果AB=17,BC=16,那么AD=______.
中,AB=AC,AD为BC边上的中线,如果AB=17,BC=16,那么AD=______.
答案:15
第11题. 如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则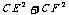 =____.
=____.
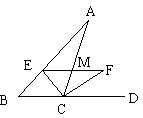
答案:25
第12题. 周长为24,斜边长为10的直角三角形面积为( )
A.12 B.16 C.20 D.24
答案:D
第13题. 如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?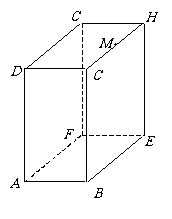
答案:25cm
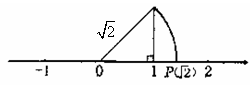
第14题. “数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是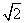 ”,这种说明问题的方式体现的数学思想方法叫做( )
”,这种说明问题的方式体现的数学思想方法叫做( )
A.代入法 B.换元法
C.数形结合 D.分类讨论
答案:C
第15题. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( ).
A.30 B.28 C.56 D.不能确定
答案:D
第16题. 在直角三角形ABC中,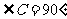 ,两直角边分别为a,b,斜边为c,如果a=5,b=12,那么c=______;如果b=8,c=17,那么三角形的面积是______.
,两直角边分别为a,b,斜边为c,如果a=5,b=12,那么c=______;如果b=8,c=17,那么三角形的面积是______.
答案:13,30
第17题. 如果直角三角形两直角边分别为a,b,斜边为c,那么它们的关系是______,即直角三角形两直角边的_______.
答案: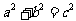 ,平方和等于斜边的平方
,平方和等于斜边的平方
第18题. 我国古代把直角三角形较短的直角边称为______,较长的直角边称为_____,斜边称为_____.
答案:勾,股,弦
第19题. 如图,下列各图中所示的线段的长度或正方形的面积为多少(各图中的三角形均为直角三角形)?
答:A=______,y=______,B=______
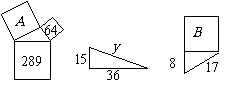
答案:225、39、225
第20题. 等腰三角形的腰长为10,底边长为12,则其底边上的高为______.
答案:8
第21题. 若一个直角三角形的三条边长是三个自然数,其中有两边的长分别为6和10,那么这个三角形的第三条边长是______.
答案:8或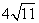
第22题. 如图,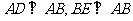 ,AB=20,AD=8,BE=12,C为AB上一点,且DC=CE,求AC.
,AB=20,AD=8,BE=12,C为AB上一点,且DC=CE,求AC.
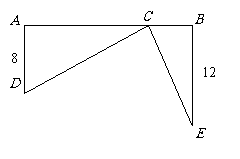
答案:12
第23题. 在直角三角形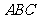 中,
中,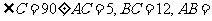 ______.
______.
答案:13
第24题. 一个三角形三个内角之比为1∶2∶1,则其相对的三边之比分别为( ).
A.1∶2∶1 B.1∶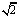 ∶1
∶1
C.1∶4∶1 D.12∶1∶2
答案:B
第25题. 已知直角三角形三边长分别为3、4、x,则x=_____.
答案:5或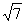
第26题. 如图,在一个由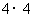 个小正方形组成的正方形网格中,阴影部分面积与正方形
个小正方形组成的正方形网格中,阴影部分面积与正方形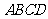 面积的比是
面积的比是
A.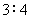 B.
B.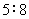
C.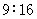 D.
D.
答案:B
12.如图,在边长为2的正方形ABCD中,P为BC边上的任意一点(点P与B、C不重合),且DQ⊥AP,垂足为Q,设AP=x,DQ=y.
(1)如果连接DP,那么△ADP的面积等于_________;
(2)当点P为BC上的一个动点时,线段DQ也随之变化,若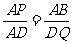 ,求y与x之间的函数关系式,并指出x的取值范围.
,求y与x之间的函数关系式,并指出x的取值范围.

11.下图中有一面围墙(可利用的最大长度为100m),现打算沿墙围成一个面积为120m2的长方形花辅.设花辅的一边AB=x(m),另一边为y(m),求y与x的函数关系式,并指出其中自变量的取值范围.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com