
题目列表(包括答案和解析)
2.已知空间三点O(0,0, 0), A(-1, 1, 0), B(0, 1, 1), 在直线OA上有一点H满足BH⊥OA,则点H的坐标为 ( )
A.(-2, 2, 0) B.(2, -2, 0) C.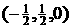 D.
D.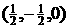
1.平行六面体 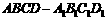 中,E,F,G,H,P,Q是
中,E,F,G,H,P,Q是 的中点,则有关系 ( )
的中点,则有关系 ( )
A.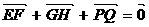 B.
B.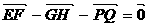
C.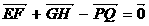 D.
D.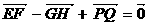
22、解:设P(x1,y1),Q(x2,y2),,则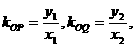
由OP⊥OQ,得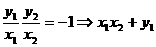 y2=0
y2=0
由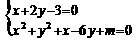 消去y,得5x2+10x+4m-27=0 ①
消去y,得5x2+10x+4m-27=0 ①
∴x1+x2=-2, x1x2=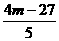 ②
②
而P,Q在直线x+2y-3=0上,则
y1y2=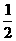 (3-x1)(3-x2)=
(3-x1)(3-x2)=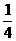 [9-3(x1+x2)+x1x2]=
[9-3(x1+x2)+x1x2]=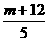 ③
③
将②,③代入x1x2+y1y2=0解得m=3,将其代入①检验,⊿>0成立,故m=3为所求。
21、 解:设李明购买磁盘、光碟分别为、张,
则由题意知: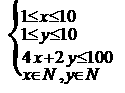
作出其表示的平面区域知其可行域内的整点(9,9)使u=4x+7y取得最大值99,此时余钱100-99=1最少,此时x=y=9,即李明应买光碟、磁盘各9张。
20、解:作OD⊥AB于D,
则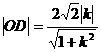 ,弦长
,弦长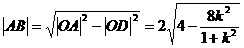
△
ABC的面积S=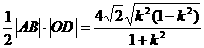 .
.
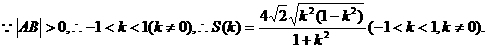
(2)设∠AOB=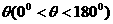 ,则
,则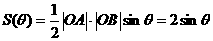
∴当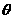 =900时,
=900时,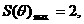 此时
此时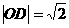 .即
.即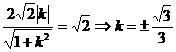
19、解:设B(x1,y1),C(x2,y2),连AG交BC于M,则M为BC的中点,
由三角形的重心公式得: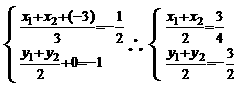 ,
,
∴点M的坐标为(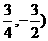 ,连结OM,则OM⊥BC,又kOM=-2,
∴kBC=
,连结OM,则OM⊥BC,又kOM=-2,
∴kBC=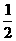 。∴BC的方程为y+
。∴BC的方程为y+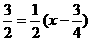 ,即4x-8y-15=0.
,即4x-8y-15=0.
(2)连结OB,在Rt△OB M中,
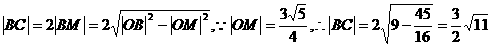
18、解:由圆心在直线2x+y=0上,设圆心坐标为(x0,-2x0)∵过点A(2,-1)且与直线x-y-1=0相切,∴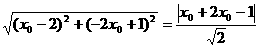 ,解得x0=1或x0=9当x0=1时,半径r=
,解得x0=1或x0=9当x0=1时,半径r=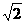 ,当x0=9时,半径r=
,当x0=9时,半径r=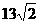 ,
,
∴所求圆的方程为:(x-1)2+(y+2)2=2或(x-9)2+(y+18)2=338
9、C 10、B 11、B 12、C
填空题:13、45 ;14.3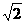 ; 15、
; 15、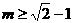 ;16、相交.
;16、相交.
解答题:17解:设l与直线2x-y-2=0交于点A1(x1,y1),则l与直线x+y+3=0交于
点(6-x1,-y1), 由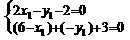 解得:x1=
解得:x1=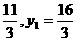 .
.
又由l经过P(3,0),A(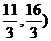 得直线l的方程为8x-y-24=0.
得直线l的方程为8x-y-24=0.
22、(14分)当m为参数时,集合A={(x,y)∣x2+y2+x-6y+m=0}是以(-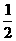 ,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
,3)为圆心的同心圆系,问m取何值时,直线x+2y-3=0与圆系中的某一个圆交于P,Q两点,满足条件OP⊥OQ(O为坐标原点).
选择题:1、D 2、B 3、A 4、C 5、A 6、B 7、B 8、C
21、(12分)李明同学准备用100元买空白磁盘和空白光碟,已知空白磁盘售价为4元/张,空白光碟的售价7元/张,问李明同学怎样设计购买方案,才能达到磁盘、光碟都买并且都不超过10张,而又使剩下的钱最少。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com