
题目列表(包括答案和解析)
18.解:(1)已知向量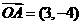 ,
,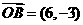 ,
,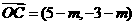 ,
,
若点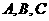 能构成三角形,则这三点不共线,即
能构成三角形,则这三点不共线,即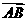 与
与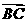 不共线. ……(4分)
不共线. ……(4分)
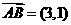 ,
,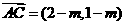 ,
,
故知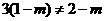 ,
,
∴实数 时,满足条件. …………………………………………………(8分)
时,满足条件. …………………………………………………(8分)
(若根据点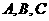 能构成三角形,必须任意两边长的和大于第三边的长,即由
能构成三角形,必须任意两边长的和大于第三边的长,即由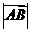
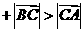 去解答,相应给分)
去解答,相应给分)
(2)若△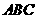 为直角三角形,且
为直角三角形,且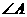 为直角,则
为直角,则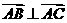 , …………(10分)
, …………(10分)
∴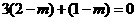 ,
,
解得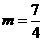 . …………………………………………………………………(13分)
. …………………………………………………………………(13分)
17.解:(1)由图可知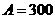 ,设
,设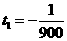 ,
,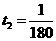 , ……………………(2分)
, ……………………(2分)
则周期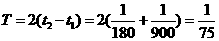 , …………………………(4分)
, …………………………(4分)
∴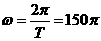 . ………………………………………………………(6分)
. ………………………………………………………(6分)
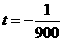 时,
时,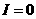 ,即
,即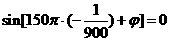 ,
,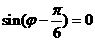 .
.
而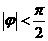 , ∴
, ∴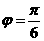 .
.
故所求的解析式为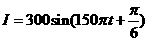 . ……………………………(8分)
. ……………………………(8分)
(2)依题意,周期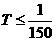 ,即
,即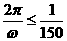 ,
,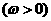 , …………………(10分)
, …………………(10分)
∴ ,又
,又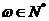 ,故最小正整数
,故最小正整数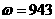 . ……………(13分)
. ……………(13分)
16.解: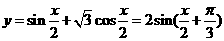 .
.
(1)最小正周期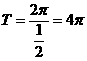 . ……………………………………………(3分)
. ……………………………………………(3分)
令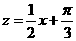 ,函数
,函数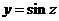 单调递增区间是
单调递增区间是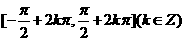 .
.
由
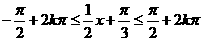 ,
,
得
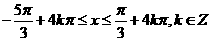 . ………………………………(5分)
. ………………………………(5分)
取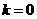 ,得
,得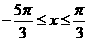 ,而
,而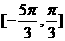
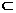
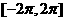 ,
,
所以,函数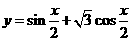 ,
,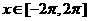 得单调递增区间是
得单调递增区间是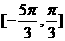 .
.
…………………………………………………………………………(8分)
(2)把函数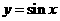 图象向左平移
图象向左平移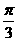 ,得到函数
,得到函数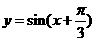 的图象,…(10分)
的图象,…(10分)
再把函数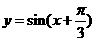 的图象上每个点的横坐标变为原来的2倍,纵坐标不变,得到函数
的图象上每个点的横坐标变为原来的2倍,纵坐标不变,得到函数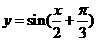 的图象, …………………………………(11分)
的图象, …………………………………(11分)
然后再把每个点的纵坐标变为原来的2倍,横坐标不变,即可得到函数
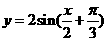 的图象. …………………………………………………(13分)
的图象. …………………………………………………(13分)
15.解:(1)因为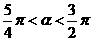 ,所以
,所以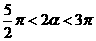 . ………………………(2分)
. ………………………(2分)
因此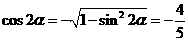 . ………………………………(4分)
. ………………………………(4分)
由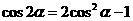 ,得
,得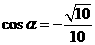 . ……………………(8分)
. ……………………(8分)
(2)因为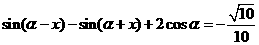 ,
,
所以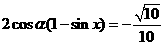 ,所以
,所以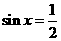 . ………………………(11分)
. ………………………(11分)
因为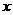 为锐角,所以
为锐角,所以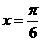 . ………………………………………………(13分)
. ………………………………………………(13分)
11. 2 12.
-13 13. 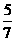 14. (1)(2)(3)
14. (1)(2)(3)
BCBBA BAAAC
20.(本小题满分13分)
已知向量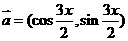 ,
,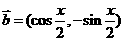 ,且
,且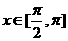 .
.
(1)求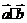 及
及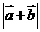 ;
;
(2)求函数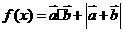 的最大值,并求使函数取得最大值时
的最大值,并求使函数取得最大值时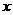 的值.
的值.
高中二年级数学级模块考试(必修4)
19.(本小题满分13分)
设平面内的向量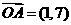 ,
,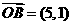 ,
,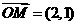 ,点
,点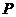 是直线
是直线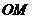 上的一个
上的一个
动点,且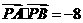 ,求
,求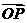 的坐标及
的坐标及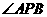 的余弦值.
的余弦值.
18.(本小题满分13分)
已知向量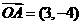 ,
,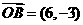 ,
,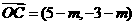 .
.
(1)若点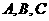 能够成三角形,求实数
能够成三角形,求实数 应满足的条件;
应满足的条件;
(2)若△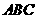 为直角三角形,且
为直角三角形,且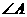 为直角,求实数
为直角,求实数 的值.
的值.
17.(本小题满分13分)
已知电流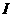 与时间
与时间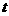 的关系式为
的关系式为 .
.
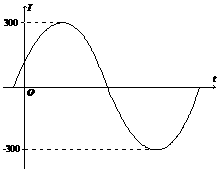 (1)下图是
(1)下图是
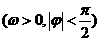 在一个周期内的图象,根据图中数据求
在一个周期内的图象,根据图中数据求 的解析式;
的解析式;
(2)如果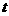 在任意一段
在任意一段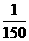 秒的时间内,电流
秒的时间内,电流
 都能取得最大值和最小值,
都能取得最大值和最小值,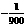
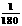
那么 的最小正整数值是多少?
的最小正整数值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com