
题目列表(包括答案和解析)
2、若从集合P到集合Q={a,b,c}所有不同的映射共有81个,则从集合Q到集合P可作的不同的映射共有( )
A.32个 B.64个 C.81个 D.27个
1、若n∈N*,则(20-n)(21-n)……(100-n)等于( )
A.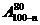 B.
B.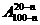 C.
C.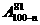 D.
D.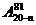
23.如图,已知 的直角顶点为
的直角顶点为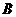 ,点
,点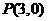 ,点
,点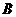 在
在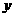 轴上,点
轴上,点 在
在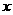 轴负半轴上,在
轴负半轴上,在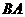 的延长线上取一点
的延长线上取一点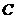 ,使
,使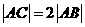 .
(1)B在
.
(1)B在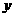 轴上移动时,求动点
轴上移动时,求动点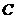 的轨迹
的轨迹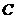 ;
;
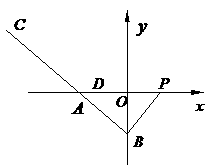 (2)若直线
(2)若直线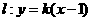 与轨迹
与轨迹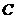 交于
交于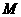 、
、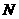 两点,设点
两点,设点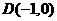 ,当
,当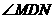 为锐角时,求
为锐角时,求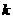 的取值范围.(14分)
的取值范围.(14分)
22.已知双曲线的中心在原点,右顶点为A(1,0),点P、Q在双曲线的右支上,点M(m,0)到直线AP
的距离为1.(1)若直线AP的斜率为k,且|k|Î[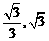 ], 求实数m的取值范围;
], 求实数m的取值范围;
(2)当m=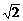 +1时,△APQ的内心恰好是点M,求此双曲线的方程.(14分)
+1时,△APQ的内心恰好是点M,求此双曲线的方程.(14分)
21.某厂生产甲、乙两种产品,生产每吨甲、乙产品所需煤、电力和所获利润如下表所示:
  消耗量 资源 消耗量 资源产品 |
煤(t) |
电力(kW) |
利润(万元) |
|
甲产品 |
9 |
4 |
12 |
|
乙产品 |
4 |
5 |
6 |
在生产这两种产品中,要求用煤量不超过350t,电力不超过220kW.问每天生产甲、乙两种产品各多少,
能使利润总额达到最大?(12分)
20.过抛物线y2=2px(p>0)的焦点F的直线与抛物线交于A、B两点,O为坐标原点,直线OA
的斜率为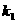 ,直线OB的斜率为
,直线OB的斜率为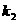 . (1)求
. (1)求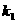 ·
·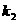 的值;
的值;
(2)过A B两点向准线做垂线,垂足分别为 、
、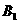 ,求
,求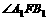 的大小.(12分)
的大小.(12分)
19.已知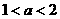 ,
,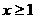 ,
,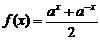 ,
,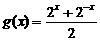 ;(1)比较
;(1)比较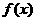 与
与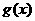 的大小;
的大小;
(2)设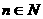 ,
,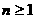 ,求证:
,求证: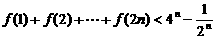 .
.
16.已知圆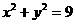 与直线
与直线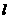 交于
交于 、
、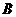 两点,若线段
两点,若线段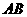 的中点
的中点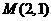
(1)求直线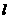 的方程; (2)求弦
的方程; (2)求弦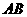 的长.(12分)
的长.(12分)
17(12分)P为椭圆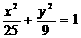 上一点,
上一点,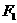 、
、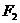 为左右焦点,若
为左右焦点,若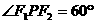
(1) 求△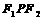 的面积; (2)求P点的坐标.(12分)
的面积; (2)求P点的坐标.(12分)
14.已知下列四个命题:
①在直角坐标系中,如果点P在曲线上,则P点坐标一定满足这曲线方程的解;
②平面内与两个定点F1,F2的距离的差的绝对值等于常数的点的轨迹叫做双曲线;
③角α一定是直线 的倾斜角;
的倾斜角;
④直线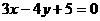 关于
关于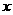 轴对称的直线方程为
轴对称的直线方程为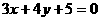 .
.
其中正确命题的序号是 (注:把你认为正确命题的序号都填上)
13.直线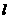 经过直线
经过直线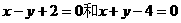 的交点,且与直线
的交点,且与直线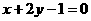 的夹角为45°,则直线
的夹角为45°,则直线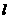 方程的一般式为 .
方程的一般式为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com