
题目列表(包括答案和解析)
8、已知⊙O半径为 ,两条直径AB,CD交成
,两条直径AB,CD交成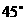 角,将圆面沿CD折成
角,将圆面沿CD折成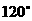 的二面角,则A,B两点此时的距离为
的二面角,则A,B两点此时的距离为
(A)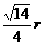 (B)
(B) 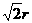 (C)
(C) 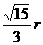 (D)
(D) 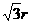
7、已知正四棱锥的侧面是正三角形,设相邻两个侧面所成的二面角为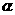 ,侧面与底面所成角为
,侧面与底面所成角为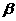 ,则
,则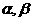 的关系是
的关系是
(A)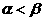 (B)
(B) 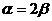 (C)
(C)
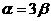 (D)
(D) 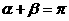
6、在直三棱柱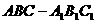 ,
,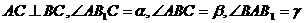 ,则有
,则有
(A)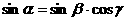 (B)
(B) 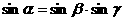
(C) 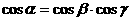 (D)
(D)

5、编号为1,2,3,4,5,6的6个不同的小球放入编号为1,2,3,4,5,6的6个不同盒子中,恰好有两个小球的编号与盒子号相同,这样不同的放法有多少种?
(A)120 (B)135 (C)180 (D)240
4、在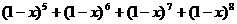 的展开式中,含
的展开式中,含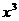 的项的系数为
的项的系数为
(A)74 (B)121 (C)-74 (D)-121
3、平行六面体中,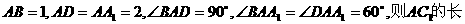
(A)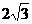 (B)
(B) 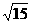 (C)4
(D)
(C)4
(D)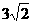
2、正四棱锥P-ABCD的所有棱长都相等,E为PC的中点,那么异面直线BE与PA所成的角的余弦值等于
(A)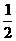 (B)
(B)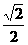 (C)
(C)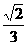 (D)
(D)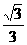
1、设a,b是两条异面直线,P为a,b外的一点,则下列结论正确的是
(A)过P有一条直线和a,b都平行。 (B) 过P有一条直线和a,b都相交。
(C)过P有一条直线和a,b都垂直 。 (D) 过P有一个平面和a,b都垂直。
21. (本小题满分14分)
有对称中心的曲线叫做有心曲线. 显然圆、椭圆、双曲线都是有心圆锥曲线. 我们称下列定义为椭圆的第三定义:
定义:直角坐标平面内的一个动点M(x,y)到两定点A1 (-a, 0), A2 (a, 0)(a≠0)的斜率乘积等于常数λ(λ<0, 且λ≠-1)的点的轨迹(连同定点A1、A2 )叫做椭圆.
⑴. 请用类似的方法写出双曲线的第三定义,并加以证明;
⑵. 请用类似的方法写出圆的定义(不必证明), 你能从上述定义中得到有心圆锥曲线(包括椭圆、双曲线、圆)的统一定义吗?请写出你的结论(不必证明).
20. (本小题满分14分)
已知椭圆C1的方程为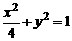 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(1). 求双曲线C2的方程;
(2). 若直线l: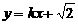 与椭圆C1及双曲线C2恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2恒有两个不同的交点,且l与C2的两个交点A和B满足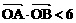 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com