
题目列表(包括答案和解析)
7. 在日常活动和科学推理中,常用的两种推理是 和
在直接证明法中,解决数学问题常用的思维方式是 和
6. 一同学在电脑中打出如下若干个圈: ○●○○●○○○●○○○○●○○○○○●…
若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●有( )个
(A)12 (B) 13 (C)14 (D)15
5.设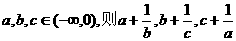
A 都不大于-2 B 都不小于-2 C 至少有一个不大于-2 D至少有一个不小于-2
4.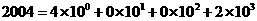 在十进制中
,那么在5进制中2004折合成十进制为 ( ) A.29 B.
254 C. 602
D. 2004
在十进制中
,那么在5进制中2004折合成十进制为 ( ) A.29 B.
254 C. 602
D. 2004
3.在下列表格中,每格填上一个数字后,使每一行
成等差数列,每一列成等比数列,则a+b+c的值是( )
|
1 |
|
2 |
|
|
|
0.5 |
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
c |
A. 1 B. 2
C. 3 D. 4
2.有这样一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”结论显然是错误的,是因为 ( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
1.若三角形能剖分为两个与自身相似的三角形,那么这个三角形的形状为( )
A .锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
13.设椭圆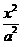 +
+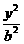 =1的两焦点为F1、F2,长轴两端点为A1、A2.
=1的两焦点为F1、F2,长轴两端点为A1、A2.
(1)P是椭圆上一点,且∠F1PF2=600,求ΔF1PF2的面积;
(2)若椭圆上存在一点Q,使∠A1QA2=1200,求椭圆离心率e的取值范围.
解:(1)设|PF1|=r1,|PF2|=r2,则S =
=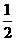 r1r2sin∠F1PF2,由r1+r2=2a,
r1r2sin∠F1PF2,由r1+r2=2a,
4c2=r12+r22-2cos∠F1PF2,得r1r2=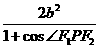 .代入面积公式,得
.代入面积公式,得
S =
=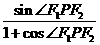 b2=b2tan∠
b2=b2tan∠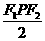 =
=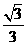 b2.
b2.
(2)设∠A1QB=α,∠A2QB=β,点Q(x0,y0)(0<y0<b). =tan(α+β)=
=tan(α+β)=  =
= 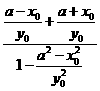 =
=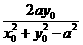 .∵
.∵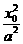 +
+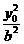 =1,∴x02=a2-
=1,∴x02=a2-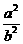 y02.
y02.
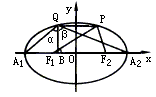 ∴tanθ=
∴tanθ=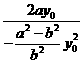 =
=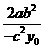 =-
=-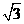 .∴2ab2=
.∴2ab2=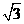 c2y0≤
c2y0≤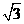 c2b, 即3c4+4a2c2-4a4≥0,
c2b, 即3c4+4a2c2-4a4≥0,
∴3e4+4e2-4≥0,解之得e2≥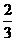 ,∴
,∴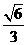 ≤e<1为所求.
≤e<1为所求.
12. 设中心在原点,焦点在x轴上的椭圆的离心率为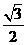 ,并且椭圆与圆x2+y2-4x-2y+
,并且椭圆与圆x2+y2-4x-2y+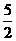 =0交于A、B两点,若线段AB的长等于圆的直径.
=0交于A、B两点,若线段AB的长等于圆的直径.
(1)求直线AB的方程;
(2)求椭圆的方程.
解:(1)设椭圆的方程为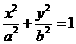 ,由
,由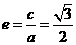 及
及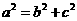 得
得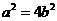 ,
,
设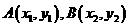 ,由于线段AB的长等于圆的直径,所以线段AB的中点为圆心(2,1),且
,由于线段AB的长等于圆的直径,所以线段AB的中点为圆心(2,1),且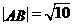 ,则
,则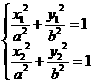 ,两式相减得
,两式相减得
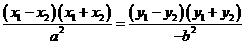 ,
,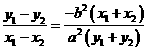 ,又
,又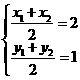 ,所以
,所以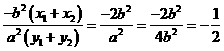 ,
,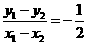 ,直线AB的方程为y=-
,直线AB的方程为y=-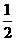 x+2;
x+2;
(2)由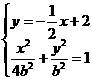 ,消去x得
,消去x得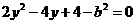 ,
,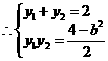 ,
,
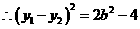 ,又
,又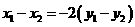 ,所以
,所以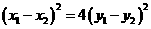 ,
,
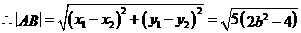 ,又
,又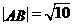 ,
,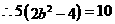 ,
,
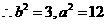 ,所求椭圆的方程为
,所求椭圆的方程为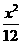 +
+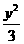 =1.
=1.
11. 已知椭圆的焦点在坐标轴上,短轴的一个端点与两焦点构成正三角形,若焦点到椭圆的最短距离为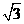 ,求椭圆的标准方程.
,求椭圆的标准方程.
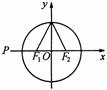 解:如图所示,设点P(
解:如图所示,设点P(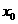 ,
,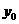 )为椭圆上位于第一象限的任一点,其到焦点距离
)为椭圆上位于第一象限的任一点,其到焦点距离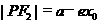 ,显然
,显然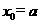 时,
时,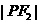 最小,故有
最小,故有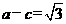 ,由短轴端点与两焦点构成正三角形得
,由短轴端点与两焦点构成正三角形得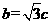 ,a=2c,解之得
,a=2c,解之得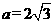 ,b=3.
,b=3.
故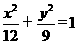 与
与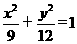 为所求椭圆方程.
为所求椭圆方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com