
题目列表(包括答案和解析)
一个棱台的侧面展开图为若干个梯形拼接而成,因此侧面积为各个梯形的面积之和,而圆台的侧面展开图为扇环,其侧面积可由大扇形的面积减去小扇形的面积而得到,所以它们的表面积公式为:
 。
。
注意区分所求的是侧面积还是表面积;再就是要认清所求的几何体是柱、锥、台中的哪一类及“棱”还是“圆”。
一个棱锥的侧面展开图是由若干个三角形拼成的,因此侧面积为各个三角形面积之和,一个圆锥的侧面展开图为扇形,利用扇形面积公式可求侧面积,所以它们的表面积公式为: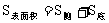 。
。
柱体的表面积是侧面面积与上、下底面面积之和。棱柱的侧面展开图是平行四边形,上、下底面不变,因此只要计算出侧面面积,其表面积可求;圆柱的侧面展开图是矩形,上、下底面不变。
设柱体的底面周长为c,高为l,则侧面积为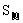 ·=c·l,故
·=c·l,故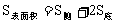 。
。
2、中心投影与平行投影的区别与联系
(1)中心投影和平行投影都是空间图形的基本画法.平行投影包括斜二测画法和三视图.中心投影后的图形与原图形相比虽然改变较多,但直观性强,看起来与人的视觉效果一致,最像原来的物体.
(2)画实际效果图时,一般用中心投影法,画立体几何中的图形时一般用平行投影法.
[典例解析]
例1. 画如图(1)(2)所示的三视图
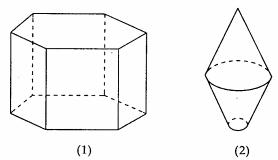
解:三视图如图(a)(b)所示
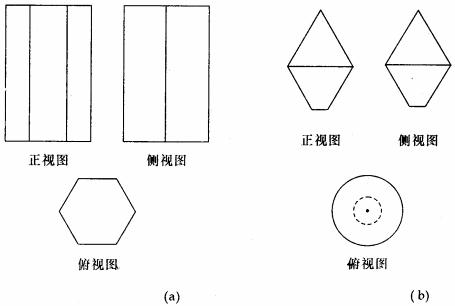
点评:(1)三视图的训练有助于我们空间能力的培养和今后应用数学知识解决工程建设、机械制造及日常生活中的问题.(2)画图时要保证“长对正、高平齐、宽相等”。
例2. 如图(1)(2)(3)是一些立体图形的视图,但是观察的方向不同,试说明下列各图可能是哪一种立体图形的视图。
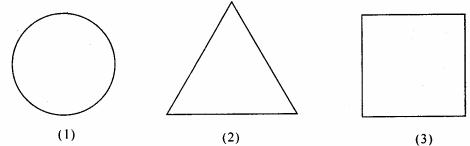
解:(1)可能为球、圆柱,如图:
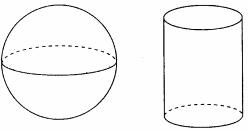
(2)可能为棱锥、圆锥、棱柱,如图:
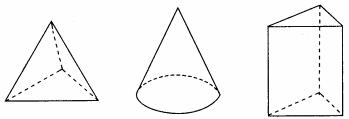
(3)可能为四棱柱,如图:
点评:这是一道综合能力较强的习题,要求学生有分类讨论的意识和对空间几何体较强的想象力。
例3. 用斜二测画法画长、宽、高分别是4cm、3cm、2cm的长方体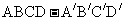 的直观图。
的直观图。
解:(1)画轴:如图。画x轴、y轴、z轴,三轴相交于点O,使∠xOz=45°,∠xOz=90°。
(2)画底面:以点O为中点,在x轴上取线段MN,使MN=4cm;在y轴上取线段PQ,使PQ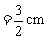 。分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD。
。分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD。
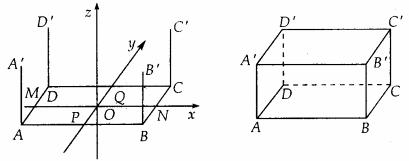
(3)画侧棱:过A、B、C、D各点分别作z轴的平行线,并在这些平行线上分别截取2cm长的线段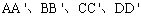
(4)成图:顺次连接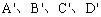 ,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图。
,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图。
点评:上述画直观图的方法称为斜二测画法,它的步骤是:
(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于点O。画直观图时,把它们画成对应的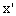 轴和
轴和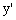 轴,两轴交于点
轴,两轴交于点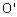 ,且使
,且使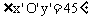 (或135°),它们确定的平面表示水平面。
(或135°),它们确定的平面表示水平面。
(2)已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于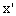 轴或
轴或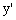 轴的线段。
轴的线段。
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变,平行于y轴的线段,长度为原来的一半。
例4. 已知正三角形ABC的边长为a,那么△ABC的平面直观图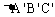 的面积为( )
的面积为( )
A.
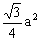 B.
B.
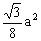 C.
C.
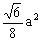 D.
D.
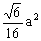
分析:先根据题意,画出直观图,然后根据直观图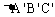 的边长及夹角求解。
的边长及夹角求解。
解:如图(1)(2)所示的实际图形和直观图,由(2)可知,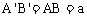 ,
,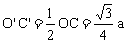 ,在图(2)中作
,在图(2)中作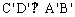 于D’,则
于D’,则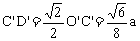
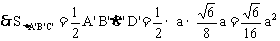
∴应选D。
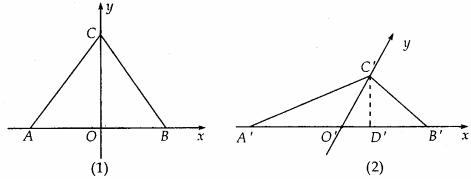
点评:本例是求直观图的面积,因此应在直观图中求解,需求出直观图的底和高,然后用三角形面积公式求解。
专题三 几种简单几何体的面积、体积
1、中心投影
一个点光源把一个图形照射到一个平面上,这个图形的影子就是它在这个平面上的中心投影.
2、斜二测画法
一种画直观图的方法,其规则是:
(1)在已知图形中建立直角坐标系xOy.画直观图时,它们分别对应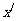 轴和
轴和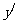 轴,两轴交于
轴,两轴交于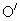 .使
.使
∠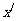 O
O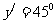 ,它们确定的平面表示水平平面.
,它们确定的平面表示水平平面.
(2)已知图形中平行于x轴和y轴的线段.在直观图中分别画成平行于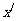 轴和
轴和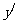 轴的线段.
轴的线段.
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度变为原来的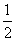 .
.
1、空间图形的直观图
用来表示空间图形的平面图形叫做空间图形的直观图.
对于简单空间几何体的组合体,一定要认真观察.先认识它的基本结构,然后再画它的三视图.
4、球的三视图都是圆.
3、圆台的正视图和侧视图都是等腰梯形,俯视图是两个同心圆.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com