
题目列表(包括答案和解析)
3.∆ABC中,已知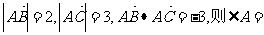 ( )
( )
A. 60O B. 120O C.300 D.1500
2.在∆ABC中,已知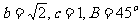 ,则a=( )
,则a=( )
A. 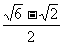 B.
B.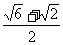 C.
C.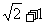 D.
D.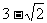
1.在∆ABC中,若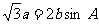 ,则B= ( )
,则B= ( )
A. 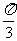 B.
B.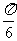 C.
C. 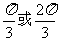 D.
D.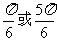
4. 解三角形的两种思想:①___________________________;②_______________________
3. 余弦定理公式:①____________________________; ②____________________________
2. S∆ABC的面积公式:____________________
1. 正弦定理公式:_________________________
2、性质
(1)两个平面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。用符合可表示为α⊥β, = l,
= l,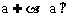 l
l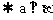 。
。
说明:①必须注意两个平面垂直的性质定理成立的条件:<1>线在面内;<2>线垂直于交线,从而可得出线面垂直。
②此定理可简述为“面面垂直,则线面垂直”,也可作为线面垂直的判定定理用。
(2)如果两个平面垂直,那么经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内。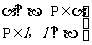
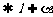 。
。
(3)如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面,即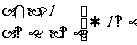 ,对于这个性质我们可以在
,对于这个性质我们可以在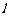 上任取一点A,过A作平面
上任取一点A,过A作平面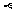 的垂线,这条直线在平面α内又在平面β内,所以这条垂线就是平面α、β的交线
的垂线,这条直线在平面α内又在平面β内,所以这条垂线就是平面α、β的交线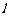 ,故
,故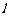 ⊥
⊥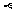 。
。
(4)三个两两垂直的平面的交线两两垂直。
即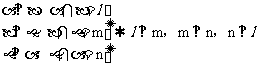 。
。
[典例解析]
例1. 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N。
(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN;
(3)若PA=AB=4,设∠BPC=θ,试用tanθ表示△AMN的面积,当tanθ取何值时,△AMN的面积最大?最大面积是多少?
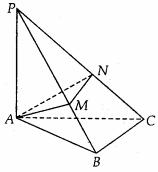
分析:本题中四面体PABC有它的特殊性,其四个面都为直角三角形,有许多垂直关系。
(1)证明:∵PA⊥平面ABC,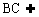 平面ABC,
平面ABC,
∴PA⊥BC,又AB为斜边,∴BC⊥AC,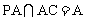 ,∴BC⊥平面PAC。
,∴BC⊥平面PAC。
(2)证明:∵BC⊥平面PAC,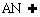 平面PAC
平面PAC
∴BC⊥AN,又AN⊥PC,且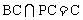
∴AN⊥面PBC,又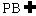 平面PBC,∴AN⊥PB
平面PBC,∴AN⊥PB
又∵PB⊥AM,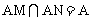 ,∴PB⊥平面AMN。
,∴PB⊥平面AMN。
(3)解:在Rt△PAB中,PA=AB=4,∴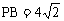
∵PA⊥AB,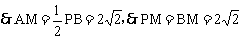
又∵PB⊥面AMN,MN 平面AMN,∴PB⊥MN
平面AMN,∴PB⊥MN
∵MN=PM·tanθ=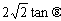 ,
,
∵AN⊥平面PBC,MN 平面PBC。∴AN⊥MN
平面PBC。∴AN⊥MN
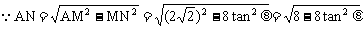
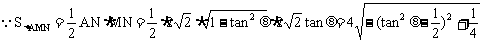
∴当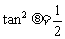 ,即
,即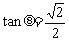 时,
时,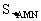 有最大值为2,
有最大值为2,
∴当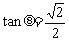 时,
时,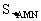 面积最大,最大值为2。
面积最大,最大值为2。
点评:(1)线线垂直 线面垂直
线面垂直
面面垂直 线面垂直,应把握常见线面垂直的方法。
线面垂直,应把握常见线面垂直的方法。
(2)一般地求最值问题首先要得到目标函数,然后借助于函数求最值的方法求出所需结果。
例2. 在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC。
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由。
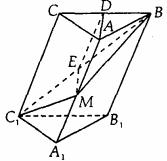
证明:(1)∵AB=AC,D是BC的中点,∴AD⊥BC,
∵底面ABC⊥平面BB1C1C,∴AD⊥侧面BB1C1C。
∴AD⊥CC1。
(2)延长B1A1与BM交于N,连结C1N,
∵AM=MA1,∴NA1=A1B1
∵A1B1=A1C1,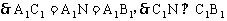
∵底面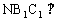 侧面BB1C1C,∴
侧面BB1C1C,∴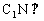 侧面BB1C1C,
侧面BB1C1C,
∴截面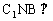 侧面BB1C1C,∴截面MBC1⊥侧面BB1C1C。
侧面BB1C1C,∴截面MBC1⊥侧面BB1C1C。
(3)结论是肯定的,充分性已由(2)证明,下面证必要性。
过M作ME⊥BC1于E,∵截面MBC1⊥侧面BB1C1C,
∴ME⊥侧面BB1C1C,又∵AD⊥侧面BB1C1C
∴ME//AD,∴M、E、D、A共面
∵AM//侧面BB1C1C,∴AM//DE
∵CC1⊥AM,∴DE//CC1
∵D是BC的中点,∴E是BC1的中点
∴AM=DE=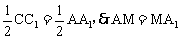
点评:(3)的结论在证必要性时,辅助线要重新作出。
[励志故事]
一分钟智慧
风来了,竹子的枝干被风吹弯;风走了,竹子又站得直直的,好像风没来过一样。
云来了,在潭底留下一道影子;云走了,潭底又干干净净的,好像云没来过一样。
竹子不会因为被风吹过,就永远直不起腰来;清澈的潭水,也不会因为云飘过,就永远留住云的影子。
同样的,心胸宽大的人,不会因为别人两句不礼貌的话,就刮起永远的狂风巨浪;也不会因为别人不礼貌的行为,就在心底刻下无法磨灭的伤痕。
1、判定
(1)定义:证明平面角为直角。
(2)判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。简述为“线面垂直,则面面垂直”,记为:l⊥β,l β=A,l
β=A,l α,则α⊥β。
α,则α⊥β。
2、面面垂直
一般地,若两平面相交,当平面角为直角时,我们称两平面垂直。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com