
1. 的相反数是( )
的相反数是( )
A.2 B.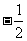 C.
C. D.
D.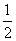
23.(本题满分14分)
如图,在平面直角坐标系xOy中,抛物线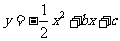 与x轴交于A(1,0)、B(5,0)两点.
与x轴交于A(1,0)、B(5,0)两点.
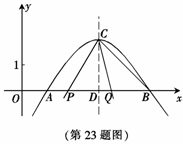
(1)求抛物线的解析式和顶点C的坐标;(4分)
(2)设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为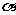 (
(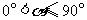 ).
).
①当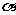 等于多少度时,△CPQ是等腰三角形?(5分)
等于多少度时,△CPQ是等腰三角形?(5分)
②设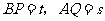 ,求s与t之间的函数关系式.(5分)
,求s与t之间的函数关系式.(5分)
22.(本题满分12分)
已知:矩形ABCD中AD>AB,O是对角线的交点,过O任作一直线分别交BC、AD于点M、N(如图①).
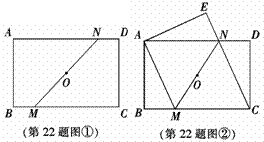

(1)求证:BM=DN;
(2)如图②,四边形AMNE是由四边形CMND沿MN翻折得到的,连接CN,求证:四边形AMCN是菱形;
(3)在(2)的条件下,若△CDN的面积与△CMN的面积比为1︰3,求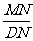 的值.
的值.
21.(本题满分12分)
为把产品打入国际市场,某企业决定从下面两个投资方案中选择一个进行投资生产。方案一:生产甲产品,每件产品成本为a万美元(a为常数,且3<a<8),每件产品销售价为10万美元,每年最多可生产200件;方案二:生产乙产品,每件产品成本为8万美元,每件产品销售价为18万美元,每年最多可生产120件。另外,年销售x件乙产品时需上交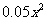 万美元的特别关税。在不考虑其它因素的情况下:
万美元的特别关税。在不考虑其它因素的情况下:
(1)分别写出该企业两个投资方案的年利润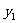 、
、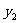 与相应生产件数
与相应生产件数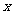 (
(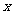 为正整数)之间的函数关系式,并指出自变量的取值范围;(4分)
为正整数)之间的函数关系式,并指出自变量的取值范围;(4分)
(2)分别求出这两个投资方案的最大年利润;(4分)
(3)如果你是企业决策者,为了获得最大收益,你会选择哪个投资方案?(4分)
20.(本题满分12分)
如图,在直角梯形ABCD中,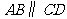 ,
,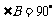 ,AB=AD,∠BAD的平分线交BC于E,连接DE.
,AB=AD,∠BAD的平分线交BC于E,连接DE.
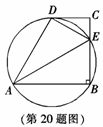
(1)说明点D在△ABE的外接圆上;(6分)
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.(6分)
19.(本题满分10分)
2009年4月1日《三明日报》发布了“2008年三明市国民经济和社会发展统计公报”,根据其中农林牧渔业产值的情况,绘制了如下两幅统计图,请你结合图中所给信息解答下列问题:
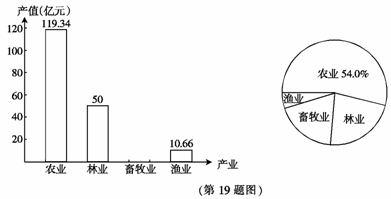
(1)2008年全市农林牧渔业的总产值为 亿元;(2分)
(2)扇形统计图中林业所在扇形的圆心角为 度(精确到度);(2分)
(3)补全条形统计图;(2分)
(4)三明作为全国重点林区之一,市政府大力发展林业产业,计划2010年林业产值达60.5亿元,求今明两年林业产值的年平均增长率. (4分)
18.(本题满分10分)
如图,A、B两点分别位于一个池塘的两端,由于受条件限制无法直接度量A、B间的距离。小明利用学过的知识,设计了如下三种测量方法,如图①、②、③所示(图中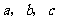 ...表示长度,
...表示长度,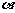 ,
,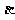 ,
,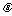 ...表示角度).
...表示角度).
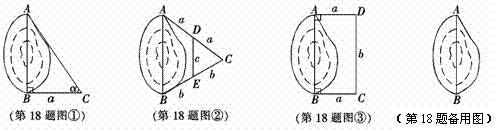

(1)请你写出小明设计的三种测量方法中AB的长度:
图①AB= ,图②AB= ,图③AB= ;(6分)
(2)请你再设计一种不同于以上三种的测量方法,画出示意图(不要求写画法),用字母标注需测量的边或角,并写出AB的长度. (4分)
17.(每小题8分,满分16分)
(1)化简: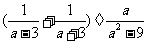 ;
;
(2)解不等式组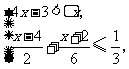 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
16.根据下列5个图形及相应点的个数的变化规律,试猜测第n个图中有 个点.
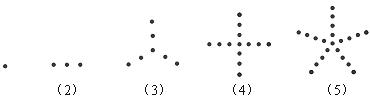
15.袋中装有2个红球和2个白球,它们除了颜色外都相同.随机从中摸出一球,记下颜色后放回袋中,再随机摸出一球,则两次都摸到红球的概率是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com