
20.(本小题满分14分)
设m>3,对于有穷数列{an}(n=1,2,…,m),令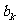 为a1,a2,…
为a1,a2,…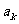 中的最大值,称数列{bn}为{an}的“创新数列”。数列{bn}中不相等项的个数称为{an}的“创新阶数”。例 如数列2,1,3,7,5的创新数列为2,2,3,7,7,创新阶数为3考查自然数1,2…,m(m>3)的所有排列,将每种排列都视为一个有穷数列{cn};
中的最大值,称数列{bn}为{an}的“创新数列”。数列{bn}中不相等项的个数称为{an}的“创新阶数”。例 如数列2,1,3,7,5的创新数列为2,2,3,7,7,创新阶数为3考查自然数1,2…,m(m>3)的所有排列,将每种排列都视为一个有穷数列{cn};
(Ⅰ)若m=5,写出创新数列为3,4,4,5,5的所有数列{cn};
(Ⅱ)是否存在数列{cn},使它的创新数列为等差数列?若存在,求出所有的数列{cn},
若不存在,请说明理由;
(Ⅲ)在创新阶数为2的所有数列{cn}中,求它们的首项的和。
19.(本小题满分14分)
已知椭圆C: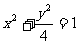 ,过点M(0,3)的直线l与椭圆C相交于两点A、B。
,过点M(0,3)的直线l与椭圆C相交于两点A、B。
(Ⅰ)若l与x轴相交于点N,且A为MN的中点,求直线l的方程;
(Ⅱ)设P为椭圆上一点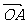 +
+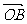 =
=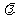
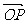 (O为坐标原点),求当|AB|<
(O为坐标原点),求当|AB|<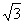 时,
时,
实数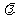 的取值范围。
的取值范围。
18.(本小题满分14分)
设a∈R,函数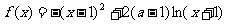
(Ⅰ)若函数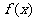 在点(0,f(0))处的切线方程为
在点(0,f(0))处的切线方程为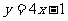 ,求
,求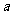 的值;
的值;
(Ⅱ)当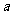 <1,讨论函数
<1,讨论函数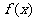 的单调性
的单调性
17.(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,,∠BCD=90°,AB∥CD,又AB=BC=PC=1,PB=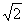 ,CD=2,AB⊥PC。
,CD=2,AB⊥PC。
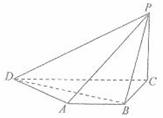
(Ⅰ)求证PC⊥平面ABCD;
(Ⅱ)求二面角B-PD-C的大小。
(Ⅲ)求点B到平面PAD的距离。
|
某个高校研究性学习小组共有9名学生,其中有3名男生和6名女生,在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言,设每人每次被选中与否均互不影响。
(Ⅰ)求两次汇报活动都是由小组成员甲发言的概率。
(Ⅱ)设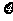 为男生发言次数与女生发言次数之差的绝对值,求
为男生发言次数与女生发言次数之差的绝对值,求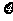 的分布列和数学期望。
的分布列和数学期望。
16.(本小题满分12分)
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为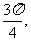
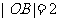 设∠AOB=
设∠AOB=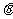 ,
,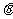 ∈(
∈(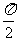 ,
,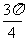 )。
)。
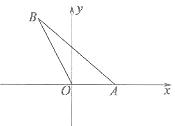
(Ⅰ)用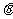 表示点B的坐标及|OA|;
表示点B的坐标及|OA|;
(Ⅱ)若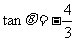 ,求
,求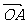 ·
·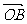 的值。
的值。
14.已知函数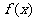 由下表给出
由下表给出
|
x |
0 |
1 |
2 |
3 |
4 |
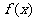 |
a0 |
a1 |
a2 |
a3 |
a4 |
其中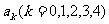 等于在a0,a1,a2,a3,a4,中k所出现的次数
等于在a0,a1,a2,a3,a4,中k所出现的次数
则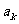 =
;a0+a1+a2+a3=
。
=
;a0+a1+a2+a3=
。
13.给出下列四个函数;
① 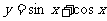 ; ②
; ②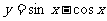 ;
;
③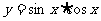 ; ④
; ④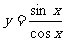 、
、
其中在(0,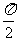 )上既无最大值又无最小值的函数是
。
)上既无最大值又无最小值的函数是
。
(写出全部正确结论的序号)
12.设O为坐标原点,向量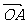 =(1,2),将
=(1,2),将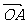 绕着点O按逆时针方向旋转90°得到向量
绕着点O按逆时针方向旋转90°得到向量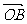 ,则2
,则2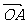 +
+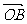 的坐标为
。
的坐标为
。
11.不等式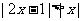 的解集为
。
的解集为
。
10.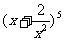 的展开式中
的展开式中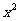 的系数是
;其展开式中各项系数之和为
的系数是
;其展开式中各项系数之和为
(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com