
7.正三棱柱ABC-A1B1C1中,D为AC的中点,AB=1、AA1=2,则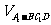 为
为
A.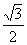 B.
B.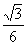 C.
C.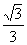 D.
D.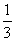
6.某办公室有8人,现从中选出3人参加A,B,C三项活动,其中甲不得参加A项活动,则不同的选派方法有
A.35种 B.56种 C.294种 D.336种
5.设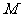 是球心
是球心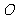 的半径
的半径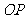 的中点,分别过
的中点,分别过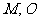 作垂直于
作垂直于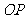 的平面,截球面得两个圆,则这两个圆的面积比值为:
的平面,截球面得两个圆,则这两个圆的面积比值为:
A.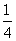 B.
B.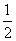 C.
C.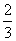 D.
D.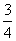
4.长方体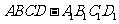 的8个顶点在同一个球面上,且AB=2,AD=
的8个顶点在同一个球面上,且AB=2,AD=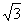 ,
,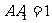 ,则顶点A、B间的球面距离是
,则顶点A、B间的球面距离是
A.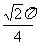 B.
B.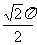 C.
C.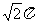 D.2
D.2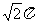
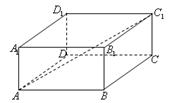
3.在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为
A.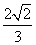 B.
B.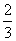 C.
C.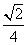 D.
D.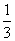
2.从5名男生和5名女生中选3人组队参加某集体项目的比赛,其中至少有一名女生入选的组队方案数为
A.100 B.110 C.120 D.180
1.设直线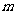 与平面
与平面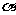 相交但不垂直,则下列说法中正确的是
相交但不垂直,则下列说法中正确的是
A.在平面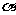 内有且只有一条直线与直线
内有且只有一条直线与直线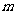 垂直
垂直
B.过直线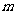 有且只有一个平面与平面
有且只有一个平面与平面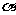 垂直
垂直
C.与直线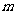 垂直的直线不可能与平面
垂直的直线不可能与平面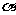 平行
平行
D.与直线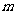 平行的平面不可能与平面
平行的平面不可能与平面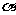 垂直
垂直
21.已知函数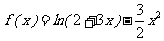 .
.
(1)求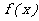 在
在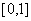 上的极值;
上的极值;
(2)若对任意x∈[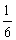 ,
,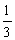 ],不等式
],不等式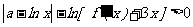 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(3)若关于x的方程f (x)= 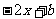 在[0, 1]上恰有两个不同的实根,求实数b的取值范围.(本题14分)
在[0, 1]上恰有两个不同的实根,求实数b的取值范围.(本题14分)
20.已知数列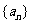 的前
的前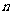 项和为
项和为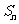 ,且有
,且有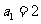 ,
,
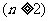 .
.
(1)求数列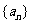 的通项公式;
的通项公式;
(2)若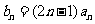 ,求数列
,求数列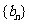 的前
的前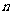 项和
项和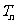 ;
;
(3)若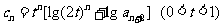 ,且数列
,且数列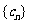 中的每一项总小于它后面的项,求实数
中的每一项总小于它后面的项,求实数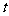 的取值范围.(本题13分)
的取值范围.(本题13分)
19.函数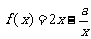 的定义域为
的定义域为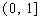 (
(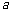 为实数)
为实数)
(1)当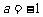 时,求函数
时,求函数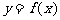 的值域;
的值域;
(2)若函数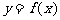 在定义域上是减函数,求
在定义域上是减函数,求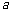 的取值范围;
的取值范围;
(3)求函数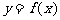 在
在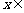
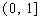 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时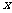 的值。
的值。
(本题12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com