
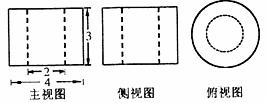
4.下图是一个空间几何体的三视图,这个几何体的体积是 ( )
A.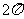 B.
B. C.
C.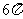 D.
D.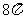
3.已知等差数列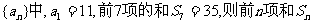 中 ( )
中 ( )
|
C.前6项和最大 D.前7项和最大
2.设集合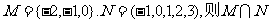 = ( )
= ( )
A.{0,1} B.{-1,0,1} C.{0,1,2} D.{-1,0,1,2}
1.已知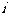 为虚数单位,则
为虚数单位,则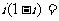 ( )
( )
A.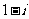 B.
B.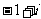 C.
C.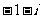 D.
D.
22.(本小题满分14分)
设函数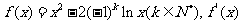 表示f(x)导函数。
表示f(x)导函数。
(I)求函数y(x)的单调递增区间;
(II)当k为偶数时,数列{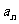 }满足
}满足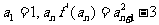 .证明:数列{
.证明:数列{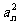 }中不存在成等差数列的三项;
}中不存在成等差数列的三项;
(III)当k为奇数时,证明:对任意正整数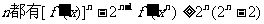 成立。
成立。
21.(本小题满分12分)
已知双曲线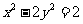 的左、右两个焦点为
的左、右两个焦点为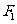 ,
, 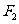 ,动点P满足|P
,动点P满足|P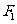 |+| P
|+| P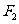 |=4.
|=4.
(I)求动点P的轨迹E的方程;
(II)设过F2且不垂直于坐标轴的动直线l交轨迹E于A、B两点,问:线段OF2上是否存在一点D,使得以DA、DB为邻边的平行四边形为菱形?作出判断并证明。
20.(本小题满分12分)
定义在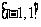 上的奇函数,已知当
上的奇函数,已知当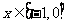 时的解析式
时的解析式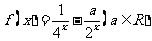
(I)写出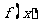 在
在 上的解析式;
上的解析式;
(II)求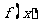 在
在 上的最大值;
上的最大值;
(III)若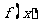 在
在 上的增函数,求实数a的取值范围。
上的增函数,求实数a的取值范围。
19.(本小题满分12分)
某中学组建A、B、C、D、E五个不同的社团组织,为培养学生的兴趣爱好,要求每个学生必须参加,且只能参加一个社团。假定某班级的甲、乙、丙三名学生对这五个社团的选择是等可能的。
(I)求甲、乙、丙三名学生参加五个社团的所有选法种数;
(II)求甲、乙、丙三人中至少有两人参加同一社团的概率;
(III)设随机变量ξ为甲、乙、丙这三个学生参加A社团的人数,求ξ的分布列与数学期望。
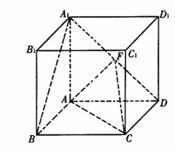
18.(本小题满分12分)
正方体ABCD-A1B1C1D1的棱长为l,点F为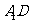 的中点.
的中点.
(I)证明: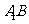 ∥平面AFC;
∥平面AFC;
(II)求二面角B-AF-C的大小。
17.(本小题满分12分)
△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),
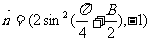 ,m⊥n。
,m⊥n。
(I)求角B的大小;
(II)若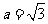 ,b=1,求c的值.
,b=1,求c的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com