
8.已知函数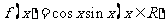 ,给出下列四个命题:
,给出下列四个命题:
①若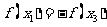 ,则
,则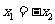 ; ②
; ②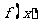 的最小正周期是
的最小正周期是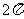
③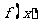 在区间
在区间 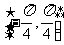 上是增函数; ④
上是增函数; ④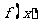 的图像关于直线
的图像关于直线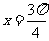 对称
对称
其中真命题是
A.①②④ B.①③ C.②③ D.③④
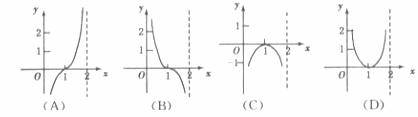
7.函数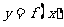 的图像如下图所示,则函数
的图像如下图所示,则函数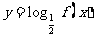 的图像大致是
的图像大致是
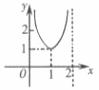
6.函数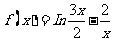 的零点一定位于区间
的零点一定位于区间
A.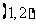 B.
B.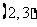 C.
C.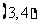 D.
D.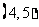
5.下图是某学校举行的运动会上,七位评委为某体操项目打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为

A.84,4.84 B.84,1.6 C.85, 1.6 D.85,4
4.如图,程序框图所进行的求和运算是
A.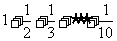 B.
B.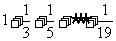
C.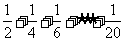 D.
D.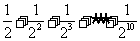
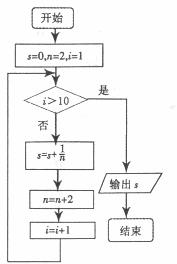
3.设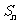 是等于差数列
是等于差数列 
A.1
B.-1 C.2 D.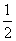
2.已知集合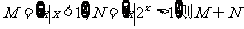 等于
等于
A.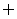 B.
B.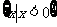 C.
C.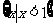 D.
D.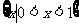
一项是符合题目要求的。
1.若将负数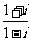 表示为
表示为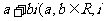 是虚数单位)的形式,则
是虚数单位)的形式,则 等于
等于
A.0 B.1 C.-1 D.2
(17)(本小题满分12分)
△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),
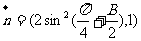 ,m⊥n,
,m⊥n,
(Ⅰ)求角B的大小;
(Ⅱ)若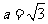 ,b=1,求c的值.
,b=1,求c的值.
(18)(本小题满分12分)
正方体ABCD-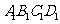 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为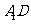 、A1C的中点.
、A1C的中点.
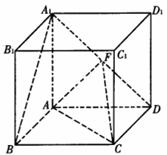
(Ⅰ)证明: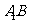 ∥平面AFC;.
∥平面AFC;.
(Ⅱ)证明B1H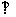 平面AFC.
平面AFC.
(19)(本小题满分12分)
定义在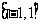 上的奇函数,已知当
上的奇函数,已知当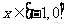 时的解析式
时的解析式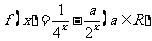
(1)写出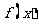 在
在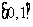 上的解析式;
上的解析式;
(2)求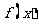 在
在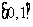 上的最大值。
上的最大值。
(20)(本小题满分12分)
从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组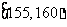 、第二组
、第二组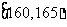 ;…第八组
;…第八组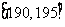 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依此构成等差数列。
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依此构成等差数列。
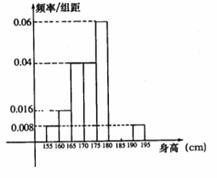
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为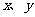 ,求满足:
,求满足: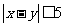 的事件概率。
的事件概率。
(21)(本小题满分12分)
已知双曲线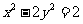 的左、右两个焦点为
的左、右两个焦点为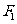 ,
, 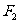 ,动点P满足|P
,动点P满足|P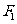 |+| P
|+| P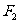 |=4.
|=4.
(1)求动点P的轨迹E的方程;
(2)设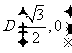 ,过
,过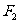 且不垂直于坐标轴的动直线l交轨迹E于A、B两点,若DA、DB为邻边的平行四边形为菱形,求直线
且不垂直于坐标轴的动直线l交轨迹E于A、B两点,若DA、DB为邻边的平行四边形为菱形,求直线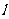 的方程
的方程
(22)(本小题满分14分)
设函数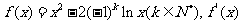 表示f(x)导函数。
表示f(x)导函数。
(Ⅰ)求函数一份(x))的单调递增区间;
(Ⅱ)当k为偶数时,数列{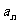 }满足
}满足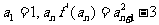 .证明:数列{
.证明:数列{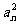 }中不存在成等差数列的三项;
}中不存在成等差数列的三项;
(Ⅲ)当k为奇数时,
设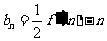 ,数列
,数列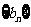 的前
的前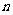 项和为
项和为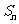 ,证明不等式
,证明不等式
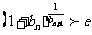 对一切正整数
对一切正整数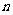 均成立,并比较
均成立,并比较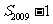 与
与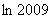 的大小。
的大小。
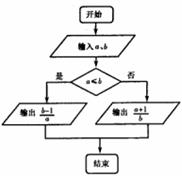
(13)对任意非零实数a、b,若a  b的运算原理如图所示,则lgl0000
b的运算原理如图所示,则lgl0000 
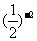 =_______。
=_______。
(14)若复数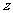 满足
满足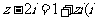 为虚数单位),则
为虚数单位),则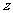 =
=
(15)若椭圆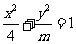 l的离心率等于
l的离心率等于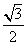 ,则____________。
,则____________。
(16)已知函数y=f(x)是R上的偶函数,对于x∈R都有f(x+60=f(x)+f(3)成立,当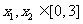 ,且
,且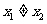 时,都有
时,都有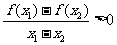 给出下列命题:
给出下列命题:
①f(3)=0;
②直线x=一6是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[一9,一6]上为增函数;
④函数y=f(x)在[一9,9]上有四个零点.
其中所有正确命题的序号为______________(把所有正确命题的序号都填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com