
2.为了了解某校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方力如图所示,根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为( )
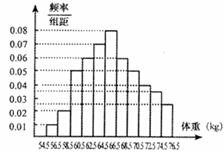
A.400 B.200 C.128 D.20
1.化简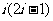 = ( )
= ( )
A.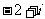 B.
B.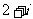 C.
C.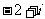 D.
D.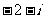
22、(本小题满分14分)
设函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同零点,求实数 a的取值范围;
(3)是否存在实数m,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由。
21、(本小题满分12分)
已知点M在椭圆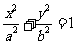 (a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点F。
(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点F。
(1)若圆M与y轴相交于A.B两点,且△ABM是边长为2的正三角形,求椭圆的方程;
(2)若点F(1,0),设过点F的直线l交椭圆于C、D两点,若直线l绕点F任意转动时恒有|OC|2+|OD|2<|CD|2,求a的取值范围。
20、(本小题满分12分)
如图,在直棱柱ABC-A1B1C1中,AC=BC=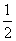 AA1,∠ACB=90º,G为BB1的中点。
AA1,∠ACB=90º,G为BB1的中点。
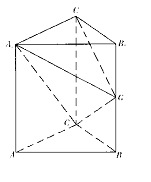
(1)求证:平面A1CG⊥平面A1GC1;
(2)求平面ABC与平面A1GC所成锐二面角的平面角的余弦值。
19、(本小题满分12分)
已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项。
(1)求数列{an}的通项公式;
(2)若bn=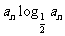 ,sn=b1+b2+┉+bn,求sn+n•
,sn=b1+b2+┉+bn,求sn+n•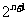 >50成立的正整数
n的最小值。
>50成立的正整数
n的最小值。
18、(本小题满分12分)
甲、乙两人进行射击训练,命中率分别为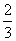 与P,且乙射击2次均未命中的概率为
与P,且乙射击2次均未命中的概率为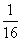 ,
,
(I)求乙射击的命中率;
(II)若甲射击2次,乙射击1次,两人共命中的次数记为ξ,求ξ的分布列和数学期望。
17、(本小题满分12分)
已知向量m=(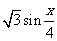 ,1),n=(
,1),n=(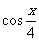 ,
,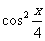 )。
)。
(1)若m•n=1,求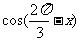 的值;
的值;
(2)记f(x)=m•n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围。
16、给出下列四个命题:
①“x(x-3)<0成立”是“|x-1|<2成立”的必要不充分条件;
②抛物线x=ay2(a≠0)的焦点为(0,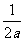 );
);
③函数f(x)=ax2-lnx的图象在x=1处的切线平行于y=x,则(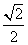 ,+∞)是f(x)的单调递增区间;
,+∞)是f(x)的单调递增区间;
④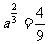 (a>0),则
(a>0),则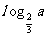 =3。
=3。
其中正确命题的序号是 (请将你认为是真命题的序号都填上)。
二 解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
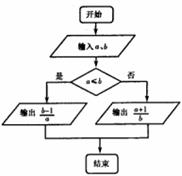
15、对任意非零实数a、b,若a  b的运算原理如图所示,则lgl0000
b的运算原理如图所示,则lgl0000 
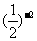 =_______。
=_______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com