
19.(本题满分12分)
如下图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且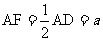 ,G是EF的中点。
,G是EF的中点。
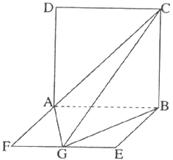
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角正弦值;
(3)求二面角B-AC-G的平面角的正弦值。
18.(本小题满分12分)
某休闲会馆拟举行“五一”庆祝活动,每位来宾交30元的入场费,可参加一次抽奖活动。抽奖活动规则是:从一个装有分值分别为1,2,3,4,5,6的六个相同小球的抽奖箱中,有放回的抽取两次,每次抽取一个球,规定:若抽得两球的分值和为12分,则获得价值为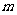 元的礼品;若抽得两球的分值和为11分或10分,则获得价值为100元的礼品;若抽得两球的分值和低于10分,则不获奖。
元的礼品;若抽得两球的分值和为11分或10分,则获得价值为100元的礼品;若抽得两球的分值和低于10分,则不获奖。
(1)求每位会员获奖的概率;
(2)假设会馆这次活动打算既不赔钱也不赚钱,则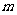 应为多少元?
应为多少元?
17.(本小题满分12分)在△ABC中,角A、B、C的对边分别为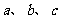 。
。
设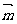
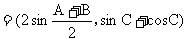 ,
,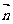
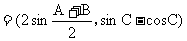 ,且
,且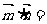
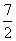 。
。
(1)求角C的大小;
(2)当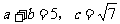 时,求△ABC的面积。
时,求△ABC的面积。
16.已知△ABC中,角A,B,C的对边分别为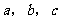 ,AH为BC边上的高,给出以下结论:①
,AH为BC边上的高,给出以下结论:①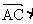
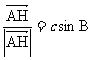 ; ②
; ②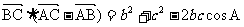 ;
③
;
③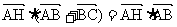 ; ④
; ④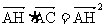 。
。
其中正确的是__________。(写出所有你认为正确结论的序号)
15.设M是△ABC内一点,且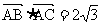 ,
,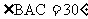 ,定义
,定义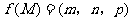 ,其中
,其中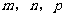 分别是△MBC,△MCA,△MAB的面积,若
分别是△MBC,△MCA,△MAB的面积,若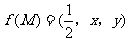 ,则
,则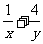 的最小值是__________。
的最小值是__________。
14.若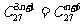 ,则
,则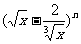 展开式中的常数项是__________。
展开式中的常数项是__________。
13.实数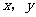 满足不等式组
满足不等式组 ,则
,则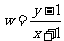 的范围__________。
的范围__________。
12.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息,设定原信息为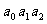 ,
,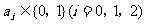 ,传输信息为
,传输信息为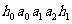 ,其中
,其中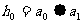 ,
,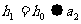 ,
, 运算规则为
运算规则为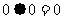 ,
,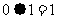 ,
,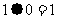 ,
,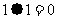 。例如原信息为111,则传输信息为01111。传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是
。例如原信息为111,则传输信息为01111。传输信息在传输过程中受到干扰可能导致接受信息出错,则下列接受信息一定有误的是
A.11010 B.01100 C.10111 D.00011
第Ⅱ卷(共90分)
11.令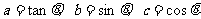 ,
,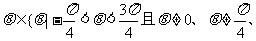
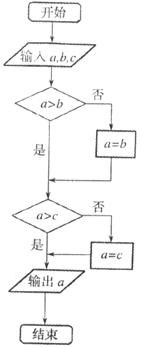
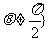 ,如下图所示的算法中,给
,如下图所示的算法中,给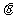 一个值,输出的为
一个值,输出的为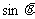 ,则
,则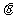 的范围是
的范围是
A.(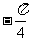 ,0) B.(0,
,0) B.(0,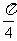 ) C.(
) C.(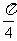 ,
,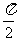 ) D.(
) D.(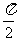 ,
,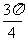 )
)
10.已知点F是双曲线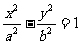
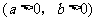 的左焦点,点E是该双曲线的右顶点,过F且垂直于
的左焦点,点E是该双曲线的右顶点,过F且垂直于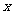 轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率
轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率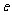 的取值范围是
的取值范围是
A.(1,+∞) B.(1,2) C.(1,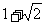 ) D.(2,
) D.(2,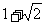 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com