2．某林场有树苗30000棵，其中松树苗4000棵．为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的数量为

A．15　　　　　　 　　　 B．20　　　　　 　C．25　　 　　　　　 D．30

1．命题“”的否命题是

A．　　　　 　B．

C．　　　　　 D．

21．(本题20分，第1小题满分4分，第2小题满分6分，第3小题6分，第4小题4分)

　　 我们知道，判断直线与圆的位置关系可以用圆心到直线的距离进行判别，那么直线与椭圆的位置关系有类似的判别方法吗？请同学们进行研究并完成下面问题。

　 (1)设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线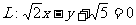的距离分别为d₁、d₂，试求d₁·d₂的值，并判断直线L与椭圆M的位置关系。

　 (2)设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线

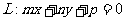　　　　 (m、n不同时为0)的距离分别为d₁、d₂，且直线L与椭圆M相切，试求d₁·d₂的值。

　 (4)将(3)中得出的结论类比到其它曲线，请同学们给出自己研究的有关结论(不必证明)。

20．(本题满分18分，第1小题满分4分，第2小题满分6分，第3小题满分8分)

　　 冬天，洁白的雪花飘落时十分漂亮。为研究雪花的形状，1904年，瑞典数学家科克(Koch Heige Von)把雪花理想化，得到了雪花曲线，也叫科克曲线。它的形成过程如下：

　 (i)将正三角形(图①)的每边三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边，得到图②；

　 (ii)将图②的每边三等分，重复上述作图方法，得到图③；

　 (iii)再按上述方法无限多次继续作下去，所得到的曲线就是雪花曲线。

　　 将图①、图②、图③……中的图形依次记作M₁、M₂、…、M_n…设M₁的边长为1。

　　 求：(1)写出M_n的边数、边长b_n、周长L_n；

　　　 (2)求M_n的面积S_n；

　　　 (3)观察上述求解的结果，数列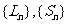有怎样的特性？它们的极限是否存在？若存在，求出极限。并归纳雪花曲线的特性。

19．(本题满分14分)

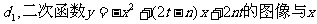　　 设m、n为正整数，且轴的两个交点间的距离为轴的两个交点间的距离为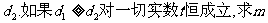、n的值。

18．(本题满分14分)

　　 在△ABC中，角A，B，C所对边分别为a，b，c，已知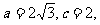　　

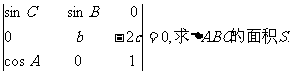
17．(本题满分12分)

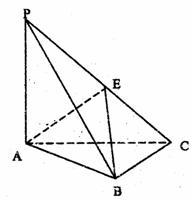
　　 如图，三棱锥P-ABC中，PA⊥平面ABC，∠BAC=60°，PA=AB=AC=2，E是PC的中点。

　 (1)求异面直线AE和PB所成角的大小；

　 (2)求三棱锥A-EBC的体积。

16．三个半径为1的球互相外切，且每个球都同时与另外两个半径为r的球外切。如果这两个半径为r的球也互相外切，则r的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 　)

15．对任意正整数n，定义n的双阶乘n！！如下：当n为偶数时，

　　 ；

　　 现有四个命题：①，②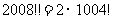，③2008！！个位数为0，④2009！！个位数为5。其中正确的个数为　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．2　　　　　　　　　　　　 C．3　　　　　　　　　　　　 D．4

14．已知非零向量则△ABC的形状是　　　　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．三边均不相等的三角形　　　　　　　　　　　 B．直角三角形

　　　 C．等腰(非等边)三角形　　　　　　　　　　　 D．等边三角形