
7.已知椭圆的中心在原点,离心率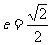 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线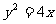 的焦点重合,则此椭圆方程为 ( )
的焦点重合,则此椭圆方程为 ( )
A.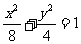 B.
B. 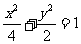 C.
C.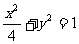 D.
D.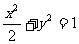
6.函数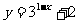
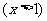 的反函数为 ( )
的反函数为 ( )
A.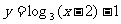
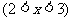 B.
B.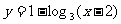
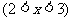
C.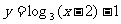
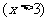 D.
D.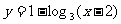
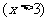
5.已知实数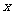 ,
,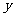 满足不等式组
满足不等式组 ,则
,则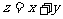 的取值范围是 ( )
的取值范围是 ( )
A.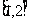 B.
B.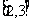 C.
C.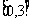 D.
D. 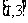
4.圆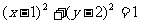 与圆
与圆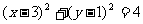 的公切线共有 ( )
的公切线共有 ( )
A.1条 B.2条 C.3条 D.4条
3.球的一个截面是半径为3的圆,球心到这个截面的距离是4,则该球的表面积是( )
A.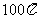 B.
B.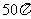 C.
C.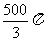 D.
D.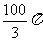
2.已知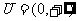 ,
,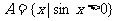 ,
,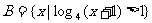 ,则
,则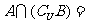 ( )
( )
A.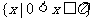 B.
B.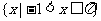
C.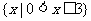 D.
D.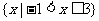
1.等差数列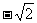 ,
,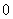 ,
,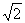 ,…的第15项为 ( )
,…的第15项为 ( )
A.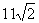 B.
B.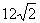 C.
C.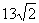 D.
D.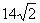
21. (本小题满分13分)已知数列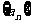 满足
满足
(Ⅰ)求数列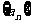 的通项公式
的通项公式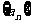 ;
;
(Ⅱ)设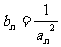 ,求数列
,求数列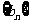 的前
的前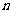 项和
项和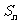 ;
;
(Ⅲ)设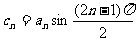 ,数列
,数列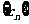 的前
的前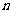 项和为
项和为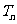 .求证:对任意的
.求证:对任意的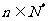 ,
,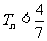 .
.
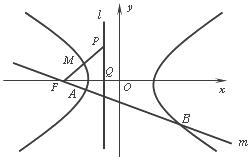
20.(本小题满分13分)如图,点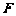 为双曲线
为双曲线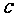 的左焦点,左准线
的左焦点,左准线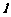 交
交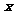 轴于点
轴于点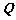 ,点P是
,点P是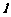 上的一点,已知
上的一点,已知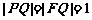 ,且线段PF的中点
,且线段PF的中点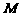 在双曲线
在双曲线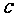 的左支上.
的左支上.
(Ⅰ)求双曲线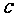 的标准方程;
的标准方程;
(Ⅱ)若过点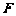 的直线
的直线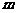 与双曲线
与双曲线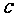 的左右两支分别交于
的左右两支分别交于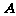 、
、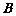 两点,设
两点,设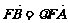 ,当
,当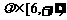 时,求直线
时,求直线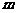 的斜率
的斜率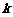 的取值范围.
的取值范围.
19. (本小题满分13分) 一位救生员站在边长为100米的正方形游泳池ABCD的A处(如图),发现C处有一位溺水者.他跑到E处后,马上跳水沿直线EC游到C处,已知救生员跑步的速度为米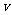 /分,游泳的速度为
/分,游泳的速度为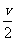 米/分.试问,救生员选择在何处入水才能最快到达C处,所用的最短时间是多少?
米/分.试问,救生员选择在何处入水才能最快到达C处,所用的最短时间是多少?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com