
18.(本小题满分12分) 甲乙二人用4张扑克牌(分别是红桃2, 红桃3, 红桃4, 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(Ⅰ)设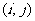 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
(Ⅱ)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜.你认为此游戏是否公平,说明你的理由.
17.(本小题满分12分)
设平面上P、Q两点的坐标分别是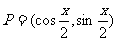 、
、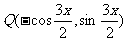 ,其中
,其中
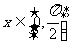 。
。
(Ⅰ)求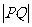 的表达式;
的表达式;
(II)记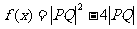 ,求函数
,求函数 的最小值和最大值。
的最小值和最大值。
16.若一个圆的圆心在抛物线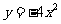 的焦点处,且此圆与直线
的焦点处,且此圆与直线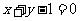 相切,则这个圆的一般方程是_________________。
相切,则这个圆的一般方程是_________________。
15.已知 是定义在
是定义在 上的减函数,其图象经过
上的减函数,其图象经过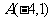 、
、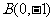 两点,则不等式
两点,则不等式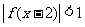 的解集是_________________。
的解集是_________________。
14.若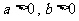 ,且
,且 ,则
,则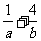 的最小值是 .
的最小值是 .
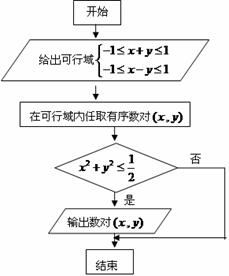
13.在可行域内任取一点规范如框图所示,则能输出数对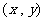 的概率是 .
的概率是 .
22.(必做题)已知等式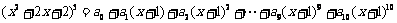 ,其中ai(i=0,1,2,…,10)为实常数.求:
,其中ai(i=0,1,2,…,10)为实常数.求:
(1)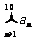 的值;
的值;
(2)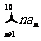 的值.
的值.
21.(选做题)从A,B,C,D四个中选做2个,每题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
A.选修4-1(几何证明选讲)
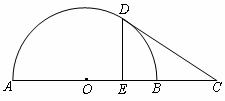
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
B.选修4-2(矩阵与变换)
将曲线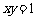 绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
绕坐标原点按逆时针方向旋转45°,求所得曲线的方程.
C.选修4-4(坐标系与参数方程)
求直线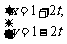 (t为参数)被圆
(t为参数)被圆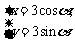 (α为参数)截得的弦长.
(α为参数)截得的弦长.
D.选修4-5(不等式选讲)
已知x,y均为正数,且x>y,求证: .
.
20.(本小题16分)
已知等差数列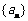 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列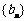 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且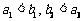 .
.
(1)求a的值;
(2)若对于任意的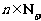 ,总存在
,总存在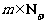 ,使得
,使得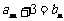 成立,求b的值;
成立,求b的值;
(3)令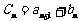 ,问数列
,问数列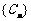 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
B.附加题部分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com