21．(本小题满分14分)

如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB，PB的中点.

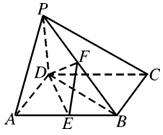
(1)求证：EF⊥CD；

(2)在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论.

(3)求DB与平面DEF所成角的正弦值.

20．(本小题满分12分)

已知抛物线方程为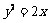，在y轴上截距为2的直线l与抛物线交于M、N两点，O为坐标原点，若OM⊥ON，求直线l的方程．

19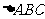．的顶点A(-5,0)，B(5,0)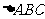，的内切圆圆心在直线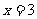上，则顶点C的轨迹是_______________(什么曲线)．

18．在三棱锥A－BCD中，平面ABD⊥平面BCD，∠BDC＝90°，E、F分别是AD、BC的中点，若EF＝CD，则EF与平面ABD所成的角为___________．

17．(本小题10分)

如图，四面体ABCD中，O、E分别是BD、BC的中点，

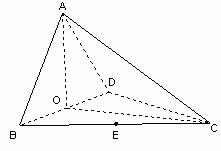
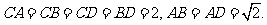
　　　　 (Ⅰ)求证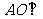：平面BCD；

　　　　 (Ⅱ)求点E到平面ACD的距离。

第Ⅱ卷(共5题，50分)

16．(本小题10分)

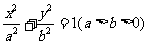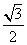　　 已知椭圆的离心率为，短轴一个端点到右焦点的距离为.

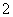(Ⅰ)求该椭圆的方程；

(Ⅱ)若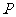是该椭圆上的一个动点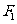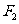，、分别是椭圆的左、右焦点，求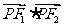的最大值与最小值.

15．(本小题10分)

设α，β是方程x²－ax+b=0的两个实根，试分析a>2且b>1是两根α、β均大于1的什么条件？

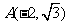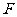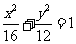14．已知定点，是椭圆的右焦点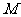，为椭圆上一点，使取得最小值，M点坐标为　　　　　　　　　　　 。

13．以抛物线y²=4x的焦点为圆心，且被抛物线的准线截得的弦长为2的圆的方程是　　　 　　　　　　　　　　　．

12．边长为2的正方形ABCD的边CD在平面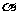内，AB在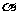平面外，如果AB与平面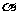的距离为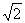，则对角线AC与平面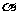所成角的大小是_____________.