
6.已知等比数列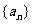 的前三项依次为
的前三项依次为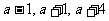 ,则
,则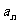 =
( )
=
( )
A.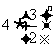 B.
B.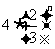 C.
C.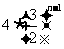 D.
D.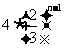
5.设点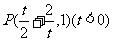 是角
是角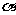 终边上一点,当
终边上一点,当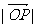 最小时,
最小时,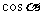 的值是 ( )
的值是 ( )
A.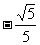 B.
B. 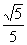 C.
C. 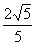 D.
D. 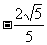
4.函数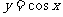 的一个单调递增区间为 ( )
的一个单调递增区间为 ( )
A.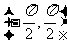 B.
B.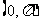 C.
C.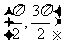 D.
D.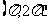
3.从某班学生中任意找出一人,如果该同学的身高小于160cm的概率为0.2,该同学的身高在[160,175]cm的概率为0.5,那么该同学的身高超过175cm的概率为( )
A.0.2 B.0.3 C.0.7 D.0.8
2.已知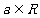 ,则“
,则“ ”是“
”是“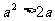 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.设全集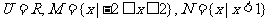 ,则
,则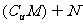 等于 ( )
等于 ( )
A. 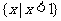 B.
B. 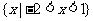
C. 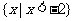 D.
D. 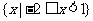
22.(本小题满分14分)
已知函数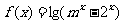
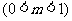 。
。
(Ⅰ)当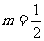 时,求
时,求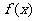 的定义域;
的定义域;
(Ⅱ)试判断函数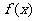 在区间(-∞,0)上的单调性并给出证明;
在区间(-∞,0)上的单调性并给出证明;
(Ⅲ)若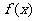 在
在 上恒取正值,求
上恒取正值,求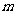 的取值范围。
的取值范围。
21.(本小题满分12分)
如下图所示,SA垂直于正方形ABCD所在的平面,P为SD上一点,且SA=AB=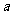 。
。
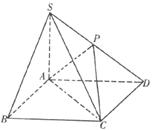
(Ⅰ)求证:AP⊥CD;
(Ⅱ)若三棱锥A-PCD的体积等于四棱锥S-ABCD的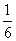 ,试确定P点的位置。
,试确定P点的位置。
20.(本小题满分12分)
某旅游公司的最大接待量为1000(人),为保证公司正常运作,实际的接待量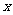 要小于1000,留出适当的空闲量[如:当接待量为800(人)时,则空闲量为200(人)],空闲量与最大接待量的比值叫空闲率。已知该公司4月份接待游客的日增加量
要小于1000,留出适当的空闲量[如:当接待量为800(人)时,则空闲量为200(人)],空闲量与最大接待量的比值叫空闲率。已知该公司4月份接待游客的日增加量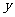 (人)和实际接待量
(人)和实际接待量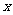 (人)与空闲率的乘积成正比。(设比例系数
(人)与空闲率的乘积成正比。(设比例系数 )
)
(Ⅰ)写出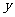 关于
关于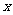 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(Ⅱ)当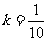 时,求4月份游客日增加量的最大值。
时,求4月份游客日增加量的最大值。
19.(本小题满分12分)
如下图,在正三棱柱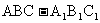 中,D为AB的中点。
中,D为AB的中点。
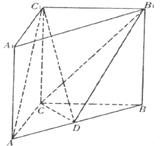
求证:(Ⅰ)AB⊥平面CDC1;
(Ⅱ)AC1∥平面B1CD。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com