
20.(本小题满分12分)已知函数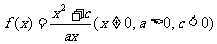 ,当
,当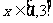 时,函数
时,函数 的取值范围恰为
的取值范围恰为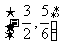 。
。
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若向量m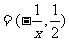 ,n
,n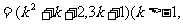 且
且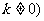 ,解关于
,解关于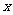 的不等式
的不等式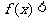 mn.
mn.
19.(本小题满分12分)某果园将一批水果用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由果园承担。
若果园恰能在约定日期(×月×日)将水果送到,则销售商一次性支付给果园20万元;若在约定的日期前送到,每提前一天销售商将多支付给果园1万元;若在约定日期后送到,每迟到一天销售商将少支付给果园1万元。
为保证水果新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送水果。已知下表内的信息:
|
统计信息 汽车行驶路线 |
不堵车的情况下到达城市乙所需时间(天) |
堵车的情况下到达城市乙所需时间(天) |
堵车的概率 |
运费(万元) |
|
公路I |
2 |
3 |
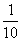 |
1.6 |
|
公路II |
1 |
4 |
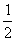 |
0.8 |
(Ⅰ)记汽车走公路Ⅰ时果园的毛利润为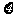 (单位:万元),求
(单位:万元),求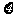 的分布列和数学期望
的分布列和数学期望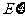 ;
;
(Ⅱ)假设你是果园的决策者,你选择哪条公路运送水果有可能让果园获得的毛利润更多?
注:毛利润=销售商支付给果园的费用-运费。
18.(本小题满分12分)如图⑴,在等腰梯形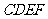 中,已知
中,已知
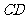 ∥
∥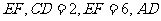 、
、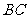 均为梯形的高,且
均为梯形的高,且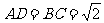 ,现沿
,现沿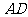 、
、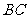 将
将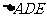 和
和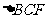 折起,使点
折起,使点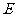 、
、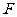 重合为一点
重合为一点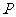 ,如图⑵所示。又点
,如图⑵所示。又点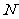 为线段
为线段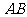 的中点,点
的中点,点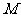 在线段
在线段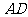 上,且
上,且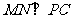 。
。
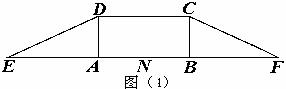
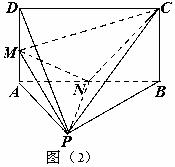
(Ⅰ)求线段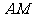 的长;
的长;
(Ⅱ)求二面角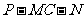 的大小。
的大小。
17.(满分12分)在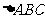 中,内角
中,内角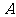 、
、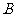 、
、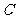 所对的边分别为
所对的边分别为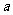 、
、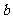 、
、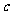 ,已知
,已知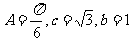 。
。
(Ⅰ)求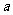 的长及
的长及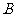 的大小;
的大小;
(Ⅱ)若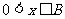 ,求函数
,求函数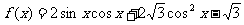 的值域。
的值域。
16.定义集合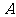 与
与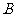 的差集
的差集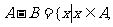 且
且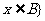 .记“从集合
.记“从集合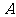 中任取一个元素
中任取一个元素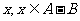 ”为 事件
”为 事件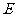 ,“从集合
,“从集合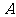 中任取一个元素
中任取一个元素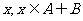 ”为事件
”为事件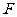 ;
;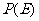 为事件
为事件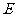 发生的概率,
发生的概率,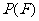 为事件
为事件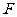 发生的概率。当
发生的概率。当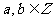 ,且
,且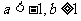 时,设集合
时,设集合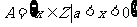 ,集合
,集合 ,给出以下判断:
,给出以下判断:
①当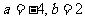 时,
时,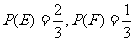 ;
;
②总有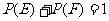 成立;
成立;
③若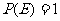 ,则
,则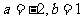 ;
;
④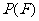 不可能等于1.
不可能等于1.
其中所有判断不正确的序号为
15.设函数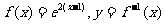 为
为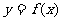 的反函数,若函数
的反函数,若函数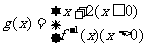 ,则
,则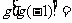
14.设地球半径为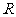 ,甲、乙两地均在本初子午线(00度经线),且甲地位于北纬400,乙地位于南纬800,则甲乙两地的球面距离为
。
,甲、乙两地均在本初子午线(00度经线),且甲地位于北纬400,乙地位于南纬800,则甲乙两地的球面距离为
。
13.若向量a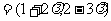 与b
与b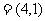 共线,则
共线,则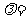 .
.
12.已知点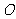 为
为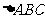 内一点,且
内一点,且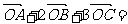 0,则
0,则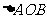 、
、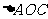 、
、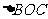 的面积之比等于 ( )
的面积之比等于 ( )
A.9:4:1 B.1:4:9 C.3:2:1 D.1:2:3
第Ⅱ卷
11.已知 ,且
,且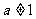 ,若函数
,若函数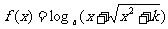 在
在 上是奇函数,又是增函数,则函数
上是奇函数,又是增函数,则函数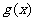
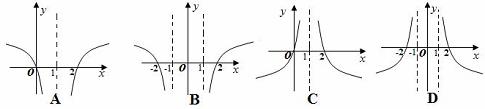
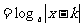 的图象是 ( )
的图象是 ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com