
22.( 本小题满分10分)
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连结EC、CD。
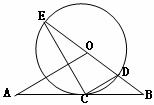
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=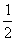 ,⊙O的半径为3,求OA的长。
,⊙O的半径为3,求OA的长。
21.(本小题满分12分)
数列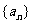 满足
满足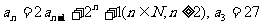 .
.
(1)求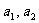 的值;
的值;
(2)是否存在一个实数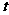 ,使得
,使得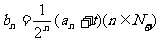 ,且数列
,且数列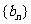 为等差数列?若存在,求出实数
为等差数列?若存在,求出实数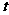 ;若不存在,请说明理由;
;若不存在,请说明理由;
(3)求数列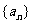 的前
的前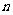 项和
项和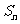 .
.
选考题:请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
20.(本小题满分12分)
如图,在棱长都相等的四面体ABCD中,点E是棱AD的中点,
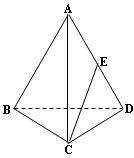
(1)设侧面ABC与底面BCD所成角为α,求tanα.
(2)设CE与底面BCD所成角为β,求cosβ.
(3)在直线BC上是否存在着点F,使直线AF与CE所成角为90°,若存在,试确定F点位置;若不存在,说明理由。
19.(本小题满分12分)
已知圆C与两坐标轴都相切,圆心C到直线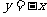 的距离等于
的距离等于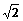 .
.
(1)求圆C的方程.
(2)若直线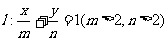 与圆C相切,求证:
与圆C相切,求证: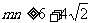 .
.
18.(本小题满分12分)
先后2次抛掷一枚骰子,将得到的点数分别记为a ,b.
(1)求直线ax+by+5=0与圆x2+y2=1相切的概率;
(2)将a,b,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
17.(本小题满分12分)
设函数f( x)=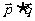 ,其中向量
,其中向量
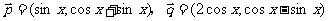 ,
,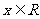 .
.
(1)求f( 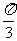 )的值及f( x)的最大值。
)的值及f( x)的最大值。
(2)求函数f( x)的单调递增区间
16.在空间中,有如下命题:
①互相平行的两条直线在同一平面内的射影必然是互相平行的两条直线;
②若平面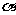 内任意一条直线
内任意一条直线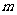 ∥平面
∥平面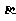 ,则
,则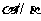 ;
;
③若平面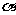 与平面
与平面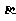 的交线为
的交线为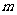 ,平面
,平面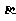 内的直线
内的直线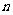 ⊥直线
⊥直线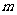 ,则
,则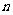 ⊥
⊥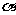 ;
;
④若点P到三角形三个顶点的距离相等,则点P在该三角形所在平面内的射影是三角形的外心;
⑤若平面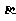 内的直线
内的直线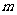 垂直于平面
垂直于平面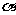 ,那么
,那么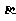 ⊥
⊥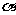 ;
;
其中正确的命题为______________。(填上所有正确命题的序号)
15.已知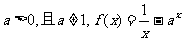 ,当
,当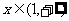 时,均有
时,均有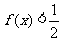 ,则实数a的取值范围为_______________.
,则实数a的取值范围为_______________.
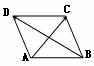
14.如图,在平行四边形ABCD中,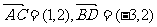 则
则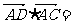 ___________。
___________。
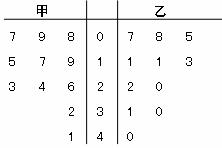
13.某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员比赛得分的中位数分别是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com