
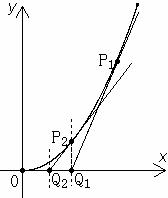
21.(本小题满分14分)如图,曲线段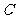 是函数
是函数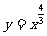
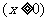 的图象,
的图象,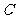 过点
过点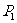
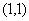 。
。
过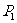 作曲线
作曲线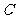 的切线交
的切线交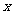 轴于
轴于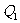 点,过
点,过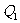 作垂直于
作垂直于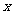 轴的直线交曲线
轴的直线交曲线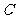 于
于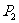
点,过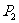 的切线交
的切线交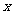 轴于
轴于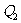 点
点 如此反复,得到一系列点
如此反复,得到一系列点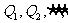
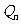 ,
,
设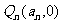 。
。
(1)
求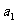 ;
;
(2)
求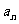 的表达式;
的表达式;
(3)
证明: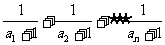
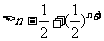 。(
。(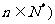
20.(本小题满分14分)设椭圆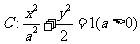 的左右焦点分别为
的左右焦点分别为 、
、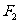 ,
,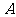 是椭圆
是椭圆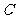 上的一点,且
上的一点,且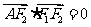 ,坐标原点
,坐标原点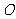 到直线
到直线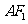 的距离为
的距离为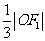 .
.
(Ⅰ)求椭圆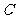 的方程;
的方程;
(Ⅱ)设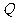 是椭圆
是椭圆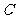 上的一点,过点
上的一点,过点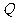 的直线
的直线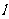 交
交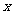 轴于点
轴于点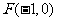 ,交
,交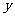 轴于点
轴于点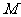 ,若
,若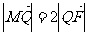 ,求直线
,求直线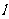 的斜率.
的斜率.
19.(本小题满分14分)已知函数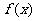 自变量取值区间
自变量取值区间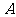 ,若其值域区间也为
,若其值域区间也为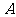 ,则称区间
,则称区间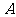 为
为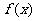 的保值区间.
的保值区间.
(Ⅰ)求函数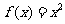 形如
形如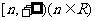 的保值区间;
的保值区间;
(Ⅱ)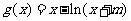 的保值区间是
的保值区间是 ,求
,求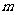 的取值范围.
的取值范围.
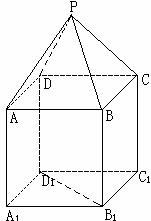
18.(本小题满分14分)如图,P-ABCD是正四棱锥,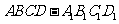 是正方体,其中
是正方体,其中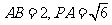

(1)求证: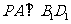 ;
;
(2)求平面PAD与平面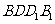 所成的锐二面角
所成的锐二面角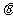 的余弦值;
的余弦值;
(3)求 到平面PAD的距离
到平面PAD的距离
17.(本小题满分12分)某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的变分布列和数学期望。
的变分布列和数学期望。
16.(本小题满分12分)函数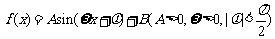 的图像上一个最高点的坐标为
的图像上一个最高点的坐标为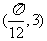 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为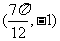 .
.
(Ⅰ)求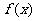 的表达式;
的表达式;
(Ⅱ)求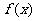 在
在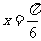 处的切线方程.
处的切线方程.
15.(不等式选讲选做题) 若不等式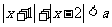 无实数解,则
无实数解,则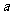 的取值范围是 .
的取值范围是 .
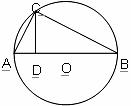
14.(几何证明选讲选做题)如图所示, 圆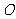 上一点
上一点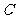 在直径
在直径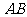 上的射影为
上的射影为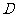 ,
, 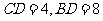 , 则圆
, 则圆 的半径等于
.
的半径等于
.
13.(坐标系与参数方程选做题)极坐标内曲线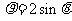 的中心
的中心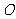 与点
与点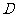
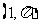 的距离为 .
的距离为 .
12.设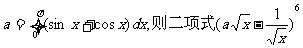 展开式中
展开式中
含x2项的系数是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com