
3.设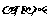 为三个不同的平面,给出下列条件:①a,b为异面直线,
为三个不同的平面,给出下列条件:①a,b为异面直线,
a ,b
,b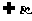 ,a//
,a//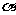 ,b//
,b//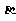 ;②
;②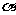 内有三个不共线的点到
内有三个不共线的点到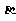 的距离相等;③
的距离相等;③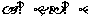 ;④
;④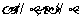 .则其中能使
.则其中能使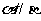 成立的条件是
成立的条件是
A.①④ B.②③ C.①③ D.②④
2.已知数列{an}为等差数列,Sn为其前n项和,且a6-a4=4, Sk= 9, a11=21,则k的值为
A.2 B.3 C.4 D.5
1.设全集U={1,a,5,7},集合M={1,a2-3a+3},CUM={5,7},则实数a的值为
A.1或3 B.1 C.3 D.以上都不对
20.(本小题满分14分)
对于三次函数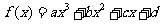
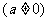 。
。
定义:(1)设 是函数
是函数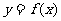 的导数
的导数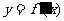 的导数,若方程
的导数,若方程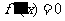 有实数解
有实数解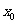 ,则称点
,则称点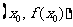 为函数
为函数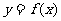 的“拐点”;
的“拐点”;
己知 ,
,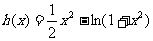 请回答下列问题:
请回答下列问题:
(1) 求函数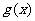 的“拐点”的坐标
的“拐点”的坐标
(2) 写出一个三次函数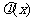 ,使得它的“拐点”是
,使得它的“拐点”是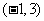 (不要写过程)
(不要写过程)
(3) 判断是否存在实数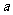 ,当
,当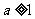 时,使得对于任意
时,使得对于任意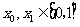 ,
, 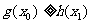 恒成立,若不存在说明理由,存在则求出a的所有的可能取值。
恒成立,若不存在说明理由,存在则求出a的所有的可能取值。
19.(本小题满分14分)
某种细菌m小时分裂一次,(每一个细菌分裂成两个,分裂所需的时间忽略不计),研究开始时仅有1个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t)
(1) 当m=1时,在所给坐标系中画出y=f(t);(0≤t<3)的图象;
(2) 当m=1时,研究进行到n小时(n≥1,n∈Z)时细菌的总数为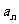 ,用关于n的式子表示
,用关于n的式子表示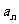 。并探究是否存在数列
。并探究是否存在数列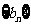 ,使得
,使得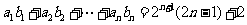 对一切正整数
对一切正整数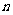 都成立?若存在,请求出数列
都成立?若存在,请求出数列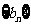 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
(3) 当m=2时,试探索研究进行到n小时(n≥0,n∈Z)时细菌的总数有多少个.(只须用关于n的式子写出结果)。
18.(本小题满分14分)
已知圆C: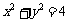 .
.
(1)直线 过点P(1,2),且与圆C交于A、B两点,若
过点P(1,2),且与圆C交于A、B两点,若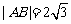 ,求直线
,求直线 的方程;
的方程;
(2)过圆C上一动点M作平行于y轴的直线m,设m与x轴的交点为N,若向量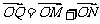 ,求动点
,求动点 的轨迹方程.
的轨迹方程.
(3) 若点R(1,0),在(2)的条件下,求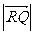 的最小值.
的最小值.
17.(本小题满分14分)
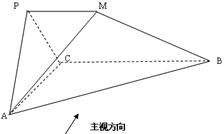
如图所示几何体中,平面PAC⊥平面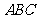 ,
,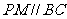 ,PA
= PC,
,PA
= PC,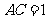 ,
,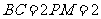 ,
,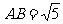 ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为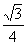 .
.
(1)求证:PA⊥BC;
(2)画出该几何体的主视图并求其面积S;
(3)求出多面体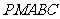 的体积V.
的体积V.
16.(本小题满分12分)
若函数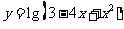 的定义域为M。当
的定义域为M。当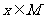 时,求
时,求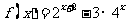 的最值及相应的x的值。
的最值及相应的x的值。
15.(本小题满分12分)
已知向量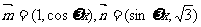 ,(
,( ),函数
),函数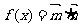 且f(x)
图像上一个最高点的坐标为
且f(x)
图像上一个最高点的坐标为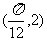 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为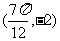 .
.
(1)求f(x)的解析式。
(2)在△ABC中,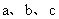 是角
是角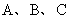 所对的边,且满足
所对的边,且满足 ,求角B的大小以及f(A)取值范围。
,求角B的大小以及f(A)取值范围。
14.数列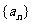 满足:
满足: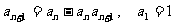 ,数列
,数列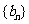 满足:
满足: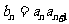 ,则数列
,则数列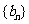 的前十项和为
.
的前十项和为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com