1．某个学院有三个系，外语系有学生1200人，数学系有学生6000人，中文系有学生2000人，现采用分层抽样的方法抽取容量为46的样本，那么在外语系、数学系、中文系中各抽取的人数分别为(　 )

　 A．6，20，2　　　 B．30，10，6 　　　C．10，6，30　　　 　D．6，30，10

20. (14分)某商场某品牌的空调每周的销售量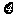是一个随机变量,分布列为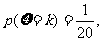 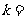11, 12, … ,30,而商场每周的进货量为区间 [11,30] 中的某一整数,商场每销售一台空调可获利500元;若供大于求,则每台多余的空调需要交保管费用100元;若供不应求,则可从其他商店调剂供应,此时每台空调仅获利200元,问此商场周初进货量应为多少时才能使周平均利润最大?

19. (14分)已知抛物线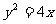,弦OP、OQ互相垂直(O为坐标原点)

(1)若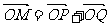,以OP的斜率为参数,求点M的轨迹的参数方程,并说明此轨迹是什么曲线.　　　

(2)证明直线PQ恒过一定点.

18. .(14分)如果有穷数列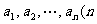为正整数)满足条件

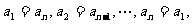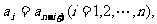即我们称其为“对称数列”，例如，由组合数组成的数列就是“对称数列”。

(1) 设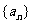是项数为5的“对称数列”.其中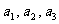是等差数列,且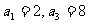,依次写出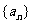的每一项.

(2)设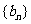是项数为9的“对称数列”,其中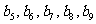是首项为1,公比为2的等比数列,求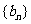各项的和.

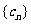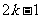(3)设是项数为(正整数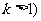的“对称数列”,其中

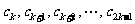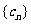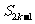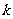是首项为50,公差为-4的等差数列,记的各项的和为,当为何值时, 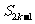有最大值?

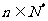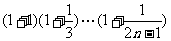17.(13分)对于任意,比较与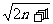的大小,并用数学归纳法证明你的结论.

16.(13分)设有关于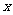的方程,其中系数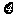是随机变量,其分布列为:

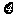	0	1	2	3	4
P	0.1	0.2	0.4	0.2	0.1

(1)　　　 求方程有实数根的概率.

(2)　　　 令随机变量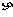表示方程的实数根的个数.(重根按一个计算).求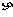的分布列.　　　　　

(3)　　　 (3)求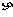的数学期望.

15.(12分)吃零食是中学生中普遍存在的问题,吃零食对学生身体发育有诸多不利影响,影响学生的健康成长.某校调查询问了56名男女学生,被调查的28名男生中喜欢吃零食的有8人,而28名女生中不喜欢吃零食的有12人,请根据所提供的数据列出列联表,并从表中的数据分析,有多大把握认为学生性别与吃零食有关.

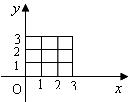
14.直角坐标系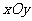中边长为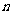(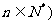的正方形,正方形内(包括边界)横坐标与纵坐标均为整数的点叫做整点.如图,当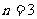时,从正方形的所有整点中随机选取1个点,该点落在正方形的对角线上的概率为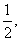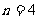时,从正方形的所有整点中随机选取1个点,该点落在正方形的对角线上的概率为_________.边长为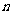(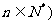时,从正方形的所有整点中随机选取1个点.则该点落在正方形的对角线上的概率为____________.

13.已知正四棱锥P-ABCD的底面边长为2,侧棱长为3,建立如图所示的空间直角坐标系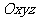,其中O为正方形ABCD的中心,则PA中点M的柱坐标为__________.

12.若直线的极坐标方程为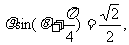则极点到该直线的距离是__________.