
5.函数y=f(x)在x=x0处可导是它在x=x0处连续的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4、质点运动规律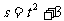 ,则在时间
,则在时间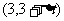 中,相应的平均速度是( )
中,相应的平均速度是( )
A. B.
B. C.
C. D.
D.
3、已知函数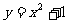 的图像上一点(1,2)及邻近一点
的图像上一点(1,2)及邻近一点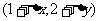 ,则
,则 等于( )
等于( )
A.2 B.2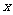 C.
C. D.2+
D.2+
2、设函数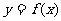 ,当自变量
,当自变量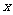 由
由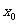 改变到
改变到 时,函数值的改变量是( )
时,函数值的改变量是( )
A.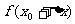 B.
B.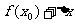 C.
C.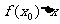 D.
D.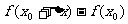
1、在函数的平均变化率的定义中,自变量的的增量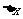 满足( )
满足( )
A.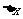 >0 B.
>0 B.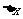 <0 C.
<0 C.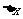
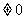 D.
D.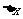 =0
=0
(17)(本小题满分12分)
已知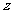 是复数,
是复数, 和
和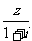 均为实数.
均为实数.
(I)求复数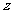 ;
;
(Ⅱ)若复数 在复平面内对应点在第二象限,求实数t的取值范围.
在复平面内对应点在第二象限,求实数t的取值范围.
(18)(本小题满分l2分)
已知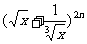 展开式的二项式系数之和比
展开式的二项式系数之和比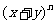 展开式的所有项系数之和大240.
展开式的所有项系数之和大240.
(I)求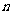 的值;
的值;
(Ⅱ)求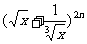 展开式的有理项.
展开式的有理项.
(19)(本小题满分12分)
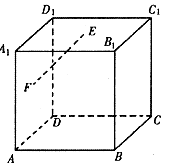
在直三棱柱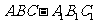 中,
中,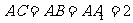 ,
,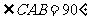 ,D、E分别是棱
,D、E分别是棱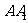 、
、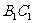 ,的中点.
,的中点.
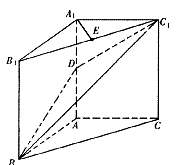
(I)求证: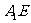 ∥平面
∥平面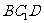 ;
;
(Ⅱ)求二面角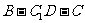 的余弦值.
的余弦值.
(20)(本小题满分12分)
某学校举办一场以“为地震灾区献爱心”为主题的图书义卖活动.同学甲随机地从l0本书中买两本,假设每本书被甲同学头走的概率相同。已知这l0本书中有3本单价足为10 元,4本单价足为15元,3本单价定为20元.记甲同学买这两本书所付金额为X(元).
(I)求甲同学所付金额为35元的概率;
(II)求随机变量X的分布列和数学期望.
(21)(本小题满分12分)
对于正数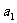 ,
,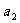 ,
,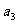 ,…,
,…,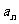 有以下不等式:
有以下不等式:
(1)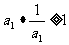
(2)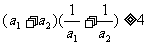
(3)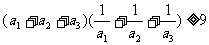
(I)给出不等式③的证明过程。
(Ⅱ)观察上面的三个不等式,猜想一般性结论,并用数学归纳法证明.
(22)(本小题满分14分)
已知函数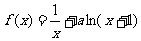 ,其中
,其中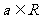 .
.
(I)若函数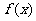 的图像在
的图像在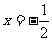 处的切线斜率
处的切线斜率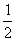 ,求
,求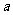 的值;
的值;
(Ⅱ)当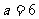 时,求函数
时,求函数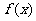 的极值;
的极值;
(Ⅲ)若 ,
,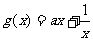 。证明:当
。证明:当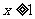 时
时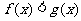 。
。
(13)曲线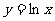 在点
在点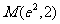 处的切线方程是
处的切线方程是
(14)已知复数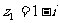 ,
,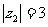 ,那么
,那么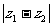 的最大值是
的最大值是
(15)由曲线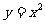 ,
,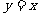 围成的平面图形的面积是
围成的平面图形的面积是
(16)边长为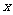 的正方形的面积
的正方形的面积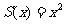 ,周长
,周长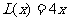 ,若将
,若将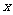 看作(0,+∞)上的变量,则
看作(0,+∞)上的变量,则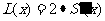 ,即
,即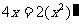 ①
①
①式可用语言叙述为:正方形面积函数的导数的2倍等于周长函数.
对于棱长为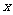 的正方体,若将
的正方体,若将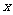 看作(0,+∞)上的变量,写出类似①的式子:
看作(0,+∞)上的变量,写出类似①的式子:
②式用语言叙述为
(1)复数 的共轭复数的虚部是
的共轭复数的虚部是
(A)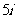 (B)
(B)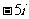 (C)
(C)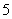 (D)
(D)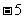
(2)AM是△A BC中BC边上的中线,设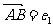 ,
,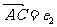 ,则
,则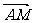 等于
等于
(A)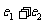 (B)
(B)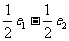 (C)
(C) (D)
(D)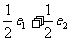
(3)若函数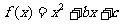 的图像的顶点在第四象限,则函数
的图像的顶点在第四象限,则函数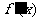 的导函数图像是
的导函数图像是
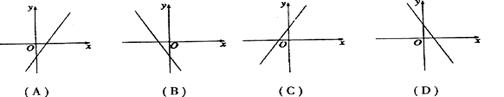
(4)已知O(0,0,0),A(1,0,0),B(0,-l,1),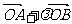 与
与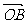 垂直,则
垂直,则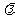 的值为
的值为
(A)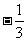 (B)0 (C)1 (D)-l
(B)0 (C)1 (D)-l
(5)甲、乙、丙、丁四位小朋友做换位游戏,开始时甲、乙、丙、丁分别坐在1、2、3、4号座位(如图),第一次前后排小朋友互换座位,第二次左右列小朋友互换座位,第三次再前后排小朋友互换座位,……,这样交替进行下去,那么第2009次互换座位后,小朋友丁的座位号是
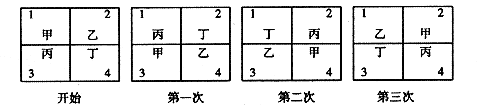
(A)1 (B)2 (C)3 (D)4
(6)抛掷红、蓝两颗骰子,设事件A=“蓝色骰子的点数为4或6”,事件B=“两颗骰子的点数之和大于9”,则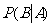 等于
等于
(A)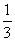 (B)
(B)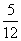 (C)
(C)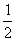 (D)
(D)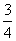
(7)某电脑销售部从5台A型笔记本电脑和6台B型笔记本电脑中选取3台捐给地震灾区,其中至少要有A型和8型的各一台,则不同的选法种数为
(A)270 (B)135 (C)80 (D)40
(8)如果函数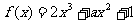 在区间(-∞,0)和(2,+∞)内单调递增,且在区间(0,2)内单调递减,则实数
在区间(-∞,0)和(2,+∞)内单调递增,且在区间(0,2)内单调递减,则实数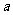 的值为
的值为
(A)1 (B)2 (C)-6 (D)-l2
(9)为迎接2008年北京奥运会,一花市要将l0盆不同的鲜花展出,其中1盆牡丹花、4盆月季,5盆君子兰,现将它们摆成一排,要求同一品种的花排在一起,并且牡丹花不排在两端,则不同的摆放种数为
(A)144 (B)288 (C)2880 (D)5760
(10)如图,正方体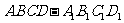 中,E、F分别是面
中,E、F分别是面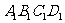 和面
和面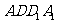 的中心,则直线EF和CD所成的角为
的中心,则直线EF和CD所成的角为
(A)60º (B)45º (C)30º (D)90º
(11)位于坐标平面点A(1,1)处的一个质点M按下述规则移动:质点每次移动一个单位;移动的方向为向上或向左,并且向上、向左移动的概率都是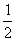 。质点M移动七次后位于点B(-3,4)处的概率为
。质点M移动七次后位于点B(-3,4)处的概率为
(A)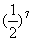 (B)
(B)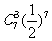 (C)
(C)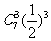 (D)
(D)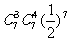
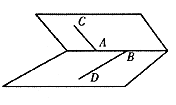
(12)如图,已知在60º的二面角的棱上有两点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4,AC=6,BD=8,则CD等于
(A)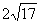 (B)
(B)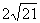 (C)
(C)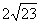 (D)
(D)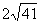
第Ⅱ卷 (非选择题 共90分)
(17)(本小题满分12分)
已知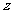 是复数,
是复数, 和
和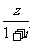 均为实数.
均为实数.
(I)求复数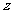 ;
;
(Ⅱ)若复数 在复平面内对应点在第二象限,求实数t的取值范围.
在复平面内对应点在第二象限,求实数t的取值范围.
(18)(本小题满分12分)
已知直线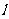 经过点P(7,
经过点P(7,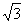 ),且与直线
),且与直线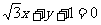 垂直.
垂直.
(I)求直线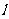 的方程;
的方程;
(Ⅱ)已知圆O的圆心在原点,若直线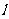 将圆O分割成弧长比为
将圆O分割成弧长比为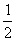 的两段圆弧,求圆O的方程.
的两段圆弧,求圆O的方程.
(19)(本小题满分12分)
对于正数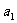 ,
,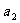 ,
,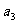 ,…,
,…,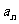 有以下不等式:
有以下不等式:
(1)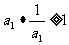
(2)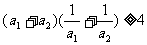
(3)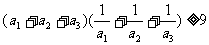
(I)观察上述三个不等式。猜想出一般性结论;
(Ⅱ)对上述不等式(3)请给出证明过程.
(20)(本小题满分12分)
某工厂生产某种产品。已知该产品的月产量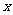 (吨)与每吨产品的价格
(吨)与每吨产品的价格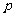 (元/吨)之间的关系为
(元/吨)之间的关系为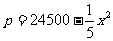 ,且生产
,且生产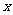 吨的成本为
吨的成本为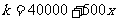 (元).
(元).
(I)求每月生产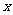 时的利润
时的利润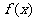 ;
;
(Ⅱ)问该厂每月生产多少吨产品才能使利润达到最大?并求出最大利润.
(21)(本小题满分12分)
命题p:方程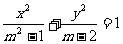 表示焦点在
表示焦点在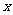 轴上的双曲线.
轴上的双曲线.
命题q:函数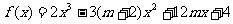 在(-∞,1)上为增函数.若“
在(-∞,1)上为增函数.若“ ”为假命题。求实数m的取值范围.
”为假命题。求实数m的取值范围.
(22)(本小题满分14分)
已知椭圆C: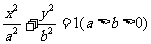 的离心率为
的离心率为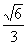 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为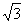 。
。
(I)求椭圆C的方程5
(II)若以k(k≠0)为斜率的直线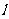 与椭圆C相交于不同的两点M、N,且线段MN的垂直平分线与两坐标轴围成三角形的面积为
与椭圆C相交于不同的两点M、N,且线段MN的垂直平分线与两坐标轴围成三角形的面积为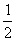 ,求
,求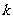 的取值范围.
的取值范围.
(13)曲线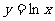 在点
在点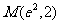 处的切线方程是
处的切线方程是
(14)已知复数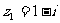 ,
,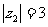 ,那么
,那么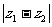 的最大值是
的最大值是
(15)已知椭圆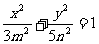 与双曲线
与双曲线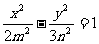 有公共的焦点,那么双曲线的渐近线方程为
有公共的焦点,那么双曲线的渐近线方程为
(16)边长为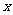 的正方形的面积
的正方形的面积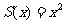 ,周长
,周长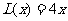 ,若将
,若将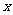 看作(0,+∞)上的变量,则
看作(0,+∞)上的变量,则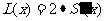 ,即
,即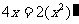 ①
①
①式可用语言叙述为:正方形面积函数的导数的2倍等于周长函数.
对于棱长为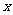 的正方体,若将
的正方体,若将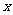 看作(0,+∞)上的变量,写出类似①的式子:
看作(0,+∞)上的变量,写出类似①的式子:
②式用语言叙述为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com