
8.已知随机变量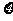 的概率分布如下:
的概率分布如下:
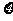 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
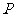 |
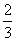 |
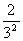 |
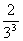 |
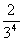 |
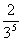 |
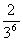 |
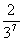 |
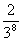 |
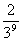 |
m |
则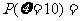
A.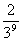 B.
B.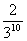 C.
C.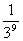 D.
D.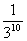
7.已知函数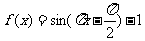 ,则下列命题正确的是
,则下列命题正确的是
A.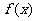 是周期为1的奇函数 B.
是周期为1的奇函数 B.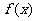 是周期为2的偶函数
是周期为2的偶函数
C.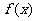 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.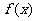 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
6.已知点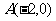 、
、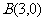 ,动点
,动点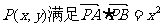 ,则点P的轨迹是
,则点P的轨迹是
A.圆 B.椭圆 C.双曲线 D.抛物线
5.甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是
p2,那么恰好有1人解决这个问题的概率是
A.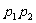 B.
B.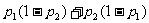
C.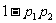 D.
D.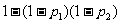
4.设复数z满足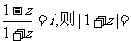
A.0 B.1 C.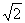 D.2
D.2
3.已知α、β是不同的两个平面,直线 ,命题
,命题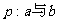 无公共点;命题
无公共点;命题
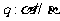 . 则
. 则 的
的
A.充分而不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分也不必要的条件
2.对于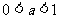 ,给出下列四个不等式
,给出下列四个不等式
①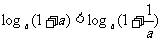 ②
②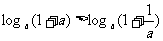
③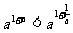 ④
④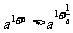
其中成立的是
A.①与③ B.①与④ C.②与③ D.②与④
一项是符合题目要求的.
1.若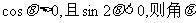 的终边所在象限是
的终边所在象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(17)(本小题满分12分)
解关于x的不等式: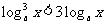 (
(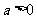 且
且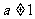 ).
).
(18)(本小题满分12分)
已知正项数列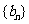 的前n项和
的前n项和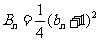 ,求
,求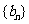 的通项公式.
的通项公式.
(19)(本小题满分12分)
已知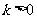 ,直线l1:y=kx,l2:y=-kx.
,直线l1:y=kx,l2:y=-kx.
(Ⅰ)证明:到l1、l2的距离的平方和为定值a(a>0)的点的轨迹是圆或椭圆
(Ⅱ)求到l1、l2的距离之和为定值c(c>0)的点的轨迹.
(20)(本小题满分12分)
已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=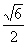 a,
a,
(Ⅰ)求异面直线AC与BC1所成角的余弦值;
(Ⅱ)求证:A1B⊥面AB1C.
(21)(本小题满分12分)
已知盒中有10个灯泡,其中8个正品,2个次品.现需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次品,求ξ的分布列及Eξ.
(22)(本小题满分14分)
已知抛物线C: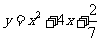 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(Ⅰ)若C在点M的法线的斜率为-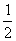 ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(Ⅱ)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
(13)抛物线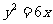 的准线方程为
.
的准线方程为
.
(14)在5名学生(3名男生,2名女生)中安排2名学生值日,其中至少有1名女生的概率是 .
(15)函数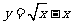 (
( )的最大值为
.
)的最大值为
.
(16)若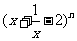 的展开式中常数项为-20,则自然数n= .
的展开式中常数项为-20,则自然数n= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com