
21.某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量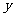 (微克)与时间
(微克)与时间 (小时)之间近似满足如图所示的曲线.
(小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后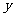 与
与 之间的函数关系式
之间的函数关系式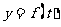 ;
;
(2)据进一步测定:每毫升血液中含药量不少于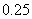 微克时,治疗有效.
微克时,治疗有效.
①求服药一次后治疗有效的时间是多长?
②当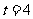 时,第二次服药,问
时,第二次服药,问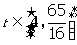 时药效能否持续?
时药效能否持续?

20.已知A、B、C为平面上不共线的三点,如图,对于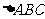 所在平面内任意一点P,设Q为线段AP的中点,R为线段BQ的中点,
所在平面内任意一点P,设Q为线段AP的中点,R为线段BQ的中点,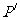 为线段RC的中点,并记
为线段RC的中点,并记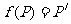 .试问
.试问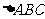 所在平面内是否存在点P,使得
所在平面内是否存在点P,使得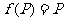 ?,若存在,请求出点P满足的条件;若不存在,请说明理由.
?,若存在,请求出点P满足的条件;若不存在,请说明理由.
19.⑴证明:当a>1时,不等式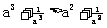 成立.
成立.
⑵要使上述不等式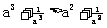 成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由.
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由.
⑶请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明.
18. 已知函数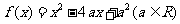
(1)如果关于 的不等式
的不等式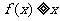 的解集为
的解集为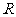 ,求实数
,求实数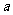 的最大值;
的最大值;
(2)在(1)的条件下,对于任意实数 ,试比较
,试比较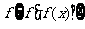 与
与 的大小;
的大小;
(3)设函数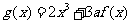 ,如果
,如果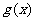 在区间
在区间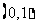 上存在极小值,求实数
上存在极小值,求实数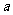 的取值范围.
的取值范围.
17.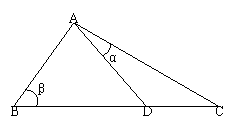 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=
如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=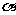 ,∠ABC=
,∠ABC=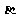 .
.
(1)证明 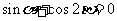 ;
;
(2)若AC=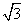 DC,求
DC,求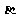 的值.
的值.
16.已知集合M是满足下列条件的函数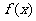 的全体:
的全体:
①当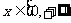 时,函数值为非负实数;
时,函数值为非负实数;
②对于任意的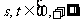 ,
,
都有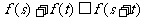 。
。
在三个函数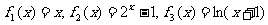 中,属于集合M的是_________.
中,属于集合M的是_________.
15.已知数列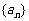 、
、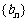 都是等差数列,
都是等差数列,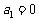 ,
,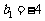 ,用
,用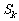 、
、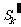 分别表示数列
分别表示数列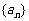 、
、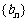 的前k项和(k是正整数),若
的前k项和(k是正整数),若 ,则
,则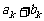 的值为_________________.
的值为_________________.
14..已知函数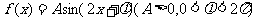 ,若对任意
,若对任意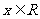 有
有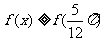 成立,则方程
成立,则方程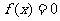 在
在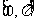 上的解为__________________.
上的解为__________________.
13.如果曲线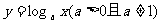 与直线y = x相切于点P,则点P的坐标是________,a = .
与直线y = x相切于点P,则点P的坐标是________,a = .
12.关于函数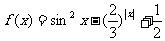 有以下四个命题:
有以下四个命题:
①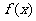 是奇函数;
②当
是奇函数;
②当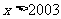 时,
时,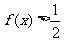 恒成立;
恒成立;
③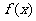 的最大值是
的最大值是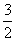 ; ④
; ④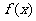 的最小值是
的最小值是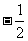 ,其中正确命题的个数是
,其中正确命题的个数是
A 1 B 2 C 3 D 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com