
9.若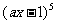 的展开式中
的展开式中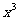 的系数是80,则实数a的值是( )
的系数是80,则实数a的值是( )
A.-2 B. 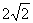 C.
C. 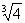 D. 2
D. 2
8. 若抛物线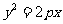 的焦点与椭圆
的焦点与椭圆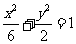 的右焦点重合,则
的右焦点重合,则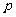 的值为( )
的值为( )
A. B.
B.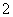 C.
C. D.
D.
7. 设向量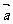 和
和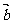 的长度分别为4和3,夹角为60°,则|
的长度分别为4和3,夹角为60°,则|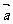 +
+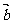 |的值为( )
|的值为( )
A.37 B.13 C.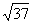 D.
D.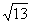
6. 极坐标方程分别是ρ=cosθ和ρ=sinθ 的两个圆的圆心距是( )
A.2
B.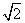 C. 1
D.
C. 1
D.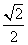
5. 一条直线若同时平行于两个相交平面,则这条直线与这两个平面交线的位置关系是( )
A.异面 B. 相交 C. 平行 D. 不确定
4.
复数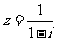 的共轭复数是( )
的共轭复数是( )
A.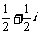 B.
B.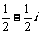 C.
C. D.
D.
3.
“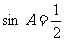 ”是“A=30º”的( )
”是“A=30º”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
2. 要从其中有50个红球的1000个形状相同的球中,采用按颜色分层抽样的方法抽取100个进行分析,则应抽取红球的个数为( )
A.5个 B.10个 C.20个 D.45个
1.已知集合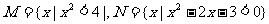 ,则集合
,则集合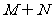 =( )
=( )
A.{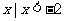 } B.{
} B.{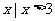 }
}
C.{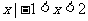 } D. {
} D. {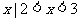 }
}
(17) (本小题满分12分)
口袋里装有红色和白色共36个不同的球,且红色球多于白色球,从袋子中取出2个球,若是同色的概率为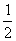 ,求(1)袋中红色、白色球各是多少?(2)从袋中任取3个球,至少一个红色球的概率是多少?
,求(1)袋中红色、白色球各是多少?(2)从袋中任取3个球,至少一个红色球的概率是多少?
(18) (本小题满分12分)
设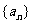 是一个公差不为零的等差数列,它的前10项和
是一个公差不为零的等差数列,它的前10项和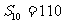 ,且
,且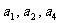 成等比数列。(1)求数列
成等比数列。(1)求数列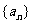 的通项公式。(2)设
的通项公式。(2)设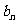 =
=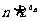 ,求数列
,求数列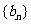 的前n项和。
的前n项和。
(19) (本小题满分12分)


 对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
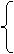 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x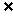 Dg
Dg
g(x)
当x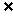 Df且x∈Dg
Df且x∈Dg
(1) 若函数f(x)=-2x+3,x≥1; g(x)=x-2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的最大值;
(3) 若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos2x,并予以证明.
(20) (本小题满分12分)
甲袋和乙袋中都装有大小相同的红球和白球,已知甲袋中共有m个球,乙袋中共有2m个球,从甲袋中摸出一个球是红球的概率为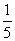 ,从乙袋中摸出一个球是红球的概率为
,从乙袋中摸出一个球是红球的概率为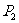 ;将甲、乙两袋球装在一起后,从中摸出一个球是红球的概率为
;将甲、乙两袋球装在一起后,从中摸出一个球是红球的概率为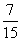 ,
,
(1)求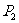 的值;
的值;
(2)从原来甲袋中摸出一个球,从原来乙袋中有放回的摸两次,每次摸一个球,求摸出的三个球中恰有2个红球的概率以及至少有1个红球的概率。
(21) (本小题满分14分)
已知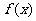 是定义在
是定义在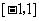 上的奇函数,且
上的奇函数,且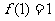 ,若m,n
,若m,n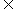
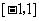 ,m+n
,m+n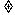 0时,有
0时,有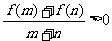 ,
,
(1)证明f(x)在[-1,1]上是增函数;
(2)解不等式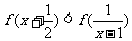
(3)若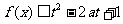 对所有x
对所有x
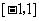 ,a
,a
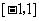 时恒成立,求实数t的取值范围。
时恒成立,求实数t的取值范围。
(22) (本小题满分14分)
已知a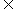 R,函数
R,函数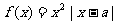
(1)当a=2时,求使f(x)=x成立的x的集合
(2)求函数y=f(x)在区间[1,2]上的最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com