
7. 椭圆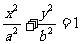 (a>b>0)的两焦点为F1、F2,连接点F1,F2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )
(a>b>0)的两焦点为F1、F2,连接点F1,F2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )
A.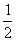 B.
B.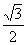 C.
C.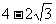 D.
D.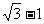
6.如图,在正四面体S-ABC中,E、F分别是SC、AB的中点,则直线EF与SA所成的角为( ).
A.90° B.60°
C.45° D.30°
5.直线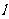 的方向向量为
的方向向量为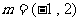 ,直线
,直线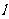 的倾角为
的倾角为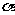 ,则
,则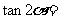 ( )
( )
A. 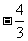 B.
B.
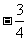 C.
C.
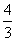 D.
D.
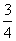
4.已知命题p:函数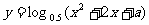 的值域为R,命题q:函数
的值域为R,命题q:函数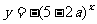 是减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是(
)
是减函数。若p或q为真命题,p且q为假命题,则实数a的取值范围是(
)
A.a 1 B.1<a<2 C.a<2 D.a
1 B.1<a<2 C.a<2 D.a 1或a
1或a 2
2
3. 若互不相等的实数a、b、c成等差数列, c、a、b成等比数列,且a+3b+c=10, 则a
等于( )
A.4 B.-2 C.2或-4 D.-4
2. 定义运算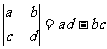 ,则符合条件
,则符合条件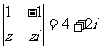 的复数z为 ( )
的复数z为 ( )
A. 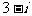 B.
B.
 C.
C.
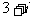 D.
D.
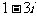
1. 已知角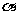 的终边过点P(-8m, -6sin30°),且cos
的终边过点P(-8m, -6sin30°),且cos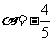 ,则m的值为 ( )
,则m的值为 ( )
A.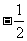 B.
B.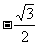 C.
C. 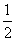 D.
D.
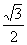
20.(本小题14分)
已知定义在(-1,1)上的函数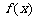 满足
满足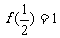 ,且对
,且对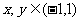 时,有
时,有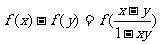 (Ⅰ)判断
(Ⅰ)判断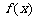 在(-1,1)上的奇偶性,并加以证明;
在(-1,1)上的奇偶性,并加以证明;
(Ⅱ)令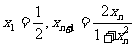 ,求数列{
,求数列{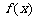 }的通项公式;
}的通项公式;
(Ⅲ)设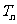 为数列{
为数列{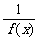 }的前
}的前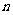 项和,问是否存在正整数
项和,问是否存在正整数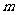 ,使得对任意的
,使得对任意的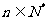 ,有
,有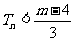 成立?若存在,求出
成立?若存在,求出 的最小值,若不存在,则说明理由。
的最小值,若不存在,则说明理由。
19.(本小题14分)
已知二次函数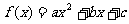
(Ⅰ)若任意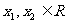 ,且
,且 ,都有
,都有 ,求证:关于
,求证:关于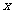 的方程
的方程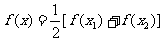 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于 ;
;
(Ⅱ)若关于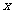 的方程
的方程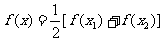 在
在 的根为
的根为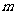 ,且
,且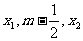 成等差数列,设函数
成等差数列,设函数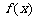 的图象的对称轴方程为
的图象的对称轴方程为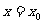 ,求证:
,求证: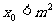 。
。
18.(本小题14分)
设关于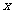 的一元二次方程
的一元二次方程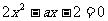 两个根为
两个根为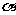 、
、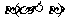 ,函数
,函数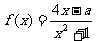
(Ⅰ)求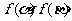 的值;
的值;
(Ⅱ)证明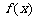 是
是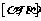 上的增函数;
上的增函数;
(Ⅲ)当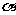 为何值时,
为何值时,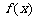 在区间
在区间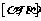 上的最大值与最小值之差最小。
上的最大值与最小值之差最小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com