20．(本小题满分14分)

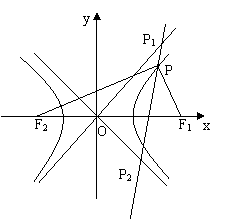
　　 如图，P是以F₁、F₂为焦点的双曲线

C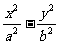： =1上一点(a>0，b>0)

已知，

　 (Ⅰ)求双曲线的离心率；

　 (Ⅱ)过点P作直线分别与双曲线的两条渐近线相交于P₁，P₂两点，或

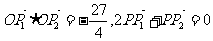　　　　 ，求双曲线C的方程.

19．(本小题满分14分)

　　 已知二次函数f(x)(x∈R)的二次项系数为正实数且满足f′(1)=0，

　 (Ⅰ)试判断函数f(x)的单调区间；

　 (Ⅱ)设向量a=(sinx，2)，b=(2sinx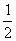，)，c=(cos2x，1)，d=(1，2).求解不等式f(a·b)>f(c·d).

18．(本小题满分14分)

　　 学校食堂定期向精英米业以每吨1500元的价格购买大米，每次购买大米需支付运输费用100元，已知食堂每天需食用大米1吨，储存大米的费用为每吨每天2元，假设食堂每次均在用完大米的当天购买.

(Ⅰ)问食堂每隔多少天购买一次大米，能使平均每天所支付的费用最少；

(Ⅱ)若购买量大，精英米业推出价格优惠措施，一次购买量不少于20吨时可享受九五折优惠，问食堂能否接受此优惠措施？请说明理由.

17．(本小题满分12分)

　　　　 如图，ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE和CE折起，使AE和BE重合，记A与B重合后的点为P，

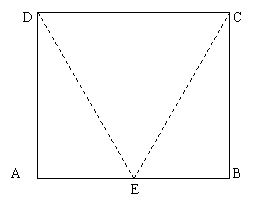　 (Ⅰ)求证：PE⊥面PCD；

　 (Ⅱ)求面PCD与面ECD所成的二面角的大小.

16．(本小题满分12分)

设a=(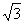sinx，cosx)，b=(cosx，cosx)，若函数f(x)=a·b+m.(m∈R)

　 (Ⅰ)指出函数f(x)的最小正周期及单调递增区间；

　 (Ⅱ)当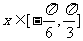时，函数f(x)的最小值为2，求此函数f(x)的最大值，并求此时的x的值.

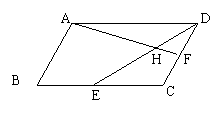
15．如图，在平行四边形ABCD中，E、F分别是BC、CD的中点，

DE与AF相交于点H, 设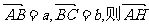等于　　　　 　.

14．函数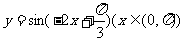的单调递增区间是　　　 　.

13．将一张坐标纸折叠一次，使得点(0，2)与点(－2，0)重合，且点(2005，2006)与点(m，n)重合，则n－m=　　　　 　.

12．记T_n=a₁·a₂·…·a_n(n∈N*)表示n个数的积，其中a_i为数列{a_n}中的第i项，若

a_n=2n－1,T₄=　　　　 　.

11．某人在黑暗中用6把钥匙随机开门，其中只有一把钥匙能把门打开，则在他在三次内(含3次)把门打开的概率是　　　　 　.