22.(本小题满分14分)

在直角坐标平面内，△ABC的两个顶点A，B的坐标分别为A(-1，0)，B(1，0)，平面内两点G，M同时满足以下条件；

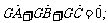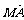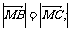①②||=③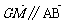

　 　 (Ⅰ)求△ABC的项点C的轨迹方程；

　 　 (Ⅱ)过点P(2，0)的直线l与△ABC的顶点C的轨迹交于E，F两点，求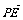·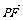的取值范围.

21.(本小题满分12分)

　 　 已知函数f(x)=x³+ax²+bx+5,在曲线y=f(x)上的点P(1，f(1))处的切线与直线y=3x+2平行.

　 　 (Ⅰ)若函数y=f(x)在x=-2时取得极值，求a,b的值；

　 　 (Ⅱ)若函数y=f(x)在区间(-2，1)上单调递增，求b的取值范围.

20.(本小题满分12分)

设数列{a_n}的各项都是正数，Sn是其前n项和，且对任意n∈N^*都有a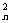=2S_n-a_n.

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若b_n=(2_n+1)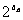,求数列{b_n}的前n项和T_n.

19.(本小题满分12分)

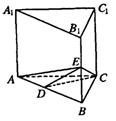　 　 如图所示，直三棱柱ABC-A₁B₁C₁中，AC=BC=AA₁=2，∠ACB=90°，E为BB₁的中点，点D在AB上且DE=.

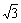　 　(Ⅰ)求证：CD⊥面A₁ABB₁；

　 　(Ⅱ)求二面角C-AE-D的大小；

　 　 (Ⅲ)求点A₁到平面CDE的距离.

18.(本小题满分12分)

甲袋中装有2个白球1个黑球，乙袋中装有3个白球1个红球，现从甲袋中连续三次有放回地摸出一球，从乙袋中连续两次有放回地摸出一球.

(Ⅰ)求从甲袋中恰有一次摸出白球同时在乙袋中恰有一次摸出红球的概率；

(Ⅱ)求从甲袋中摸出白球的次数与从乙袋中摸出白球的次数之和为2的概率；

17.(本小题满分12分)

　 　 已知向量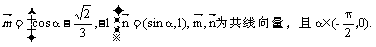

　 　 (Ⅰ)求sinα-cosα的值；

　 　 (Ⅱ)求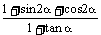的值.

16.从8个男生和6个女生中选3人去观看一场乒乓球比赛，要求至少有一名男生参加，则不同的选法共有________种.(请用数字作答)

15.如果直线l将圆x²+y²-2x-4y=0平分，且不经过第四象限，那么l的斜率的取值范围是________.

14.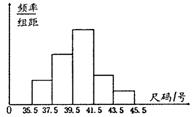为了了解商场某日旅游鞋的销售情况，抽取了

部分顾定购鞋的尺寸，将所得的数据整理后，画

出频率分布直方图如图.已知图中从左至右前3个小

组的频率之比为1∶2∶3，第4小组与第5小组的

频率分别为0.175和0.075，第二小组的频数为10，则抽取的顾客人数是________.

13.在△ABC中，∠B=30°，AC=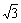，BC=3，则∠C的大小为___________.