
10.已知函数f(x)在(–1,1)上有定义,f(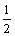 )= –1,且当x, y
)= –1,且当x, y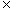 (–1,1)时,恒有f(x)+f(y)
=f(
(–1,1)时,恒有f(x)+f(y)
=f(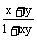 ),
),
数列{an}中a1 =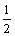 ,an+1 =
,an+1 =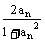 (n
(n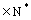 ),则f(an)等于 ( )
),则f(an)等于 ( )
A. 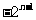 B.
B.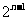 -2 C.
-2 C. +1 D.
+1 D.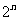 -3
-3
第Ⅱ卷 (非选择题 共100分)
9.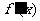 是
是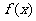 的导函数,
的导函数,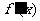 的图象如图所示,
的图象如图所示,
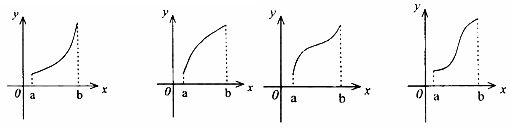 则
则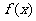 的图象只可能是( )
的图象只可能是( )
|
8.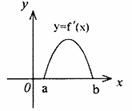 在各项均不为零的等差数列
在各项均不为零的等差数列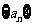 中,若
中,若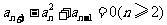 ,则
,则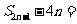 ( )
( )
A
 B
B
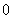 C
C
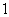 D
D
7.已知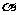 是三角形的一个内角,且
是三角形的一个内角,且 ,则方程
,则方程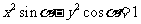 表示( )
表示( )
A.焦点在x轴上的双曲线 B.焦点在y轴上的双曲线
C.焦点在x轴上的椭圆 D.焦点在y轴上的椭圆
6.定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈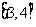 时,f(x)=x-2,则 ( )
时,f(x)=x-2,则 ( )
A.f(sin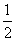 )<f(cos
)<f(cos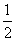 ) B.f(sin
) B.f(sin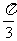 )>f(cos
)>f(cos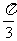 )
)
C.f(sin1)<f(cos1)
D.f(sin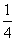 )<f(cos
)<f(cos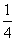 )
)
4.已知f(x)的反函数为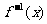 ,g(x)的图像与
,g(x)的图像与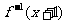 图像关于直线y=x对称,则g(x)为( )
图像关于直线y=x对称,则g(x)为( )
A.f -1(x)-1 B.f (x+1) C.f(x)+1 D.f(x)-1
|
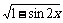 =sinx-cosx, 则 ( )
=sinx-cosx, 则 ( )
A.0≤x≤π B.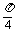 ≤x≤
≤x≤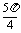 C.
C.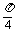 ≤x≤
≤x≤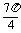 D.
D.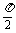 ≤x≤
≤x≤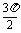
3.已知等差数列{an}中,a1>0,a5=3a7, 该数列前n项和为Sn,当Sn取得最大值时,n等于( )
A.7 B.8 C.7或8 D.6或7
2.“a=1”是“函数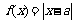 在区间
在区间 上为增函数”的 ( ) A.充分不必要条件 B.必要不充分条件
上为增函数”的 ( ) A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.设集合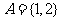 ,则满足
,则满足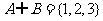 的集合B的个数是 ( )
的集合B的个数是 ( )
A.1 B.3 C.4 D.8
21.(本小题满分14分)
设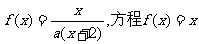 有唯一解,已知
有唯一解,已知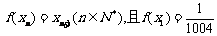
(Ⅰ)求数列{xn}的通项公式;
(Ⅱ)若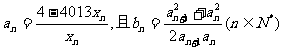 ,求和Sn=b1+b2+…+bn;
,求和Sn=b1+b2+…+bn;
(Ⅲ)是否存在最小整数m,使得对任意n∈N*,有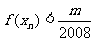 成立,若存在,求出m的值,若不存在,说明理由.
成立,若存在,求出m的值,若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com