
5.已知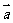 、
、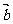 均为单位向量,它们的夹角为60°,那么
均为单位向量,它们的夹角为60°,那么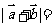 ( )
( )
A.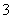 B.2 C.4
D.
B.2 C.4
D.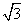
4.在等差数列 中,若
中,若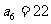 ,则
,则 的值为( )
的值为( )
A.11 B.12 C.21 D.22
3.若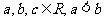 则下列不等式恒成立的是( )
则下列不等式恒成立的是( )
A.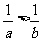 B.
B.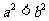 C.
C.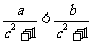 D.
D.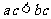
2. 已知集合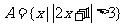 ,
,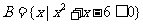 ,则
,则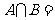 ( )
( )
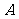
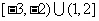
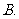

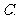
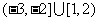
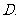

1.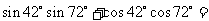 ( )
( )
A.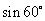 B.
B.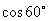 C.
C.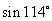 D.
D.
11.已知向量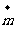 = (1―cosA, sinA)且与向量
= (1―cosA, sinA)且与向量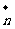 = (0 , 1)所成的角为
= (0 , 1)所成的角为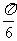 ,其中A、B、C是ΔABC的内角.
,其中A、B、C是ΔABC的内角.
(1)求角A的大小;
(2)求B + C的值,并求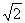 cosB + 1的取值范围.
cosB + 1的取值范围.
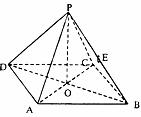
12正四棱锥P-ABCD中,侧棱PA与底面ABCD所成的角的正切值为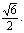
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值
(3)试在侧面PAD上寻找一点F,使EF⊥侧面PBC,确定点F的位置,并加以证明.
13(理).
设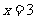 是函数
是函数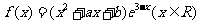 的一个极值点。
的一个极值点。
(Ⅰ)、求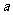 与
与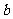 的关系式(用
的关系式(用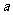 表示
表示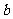 ),并求
),并求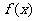 的单调区间;
的单调区间;
(Ⅱ)、设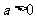 ,
,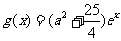 。若存在
。若存在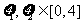 使得
使得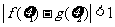 成立,求
成立,求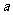 的取值范围。
的取值范围。
13(文)、已知二次函数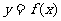 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为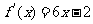 ,数列
,数列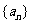 的前n项和为
的前n项和为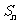 ,点
,点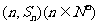 均在函数
均在函数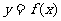 的图像上。
的图像上。
(Ⅰ)、求数列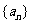 的通项公式;
的通项公式;
(Ⅱ)、设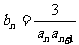 ,
,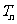 是数列
是数列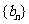 的前n项和,求使得
的前n项和,求使得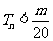 对所有
对所有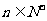 都成立的最小正整数m;
都成立的最小正整数m;
9(理).在条件 下, z= 3+2x―y的最小值是______ ___.
下, z= 3+2x―y的最小值是______ ___.
9(文).已知α∈(,π),sinα=,则tan(α+)= .
10(理).关于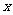 的方程
的方程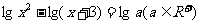 在区间(3,4)内有解,则a的取值范围是
.
在区间(3,4)内有解,则a的取值范围是
.
10(文).数学拓展课上,老师定义了一种运算“*”,对于n∈N*满足以下运算性质:(1)2*2=1,(2)(2n+2)*2=3(2n*2).则2n*2用含n的代数式表法为 .
8.关于函数f(x)=lg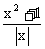 (x≠0,x∈R)有下列命题:
(x≠0,x∈R)有下列命题:
①函数y=f(x)的图象关于y轴对称。
②当x>0时,f(x)是增函数;当x<0时,f(x)是减函数。
③函数f(x)的最小值是lg2。
④当-1<x<0或x>1时,f(x)是增函数。
⑤f(x)无最大值,也无最小值。
其中正确的命题的序号是___
A ②⑤ B ①②④ C ①③④ D ①③⑤
6、如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面
A1B1C1D1的中心,则O到平面AB C1D1的距离为 ( )
A、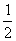 B、
B、 C、
C、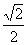 D、
D、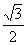
7(理).将一张画了两轴的长度单位相同的平面直角坐标系的纸折
叠一次,使点(2,0)与点(-2,4)重合,若点(7,3)
与点(m,n)重合,则m+n的值为 ( )
A.3 B.7 C.10 D.4
7(文)、已知直线x=1是函数y=f(2x)图象的一条对称轴,那么函数y= f(3-2x)的图象( )
A、关于直线x=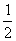 对称 B、关于直线x= -
对称 B、关于直线x= -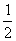 对称
对称
C、关于直线x=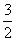 对称 D 、关于直线x= -
对称 D 、关于直线x= -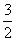 对称
对称
5、设向量a=(1,-3),b=(-2,4),若表示向量4a、3b-2a、c的有向线段首尾相接能构成三角形,则向量c为( D )
 (A)(1,-1)
(B)(-1, 1) (C) (-4,6) (D) (4,-6)
(A)(1,-1)
(B)(-1, 1) (C) (-4,6) (D) (4,-6)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com