
8.椭圆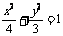 上有n个不同的点
上有n个不同的点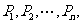 椭圆右焦点为F,数列
椭圆右焦点为F,数列 的等差数列,则n的最大值是
的等差数列,则n的最大值是
A.2003 B.2004 C.2005 D.2006
7.如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角。已知AB=2CD=4MN,给出下列四个等式: 其中成立的个数是
其中成立的个数是
A.1 B.2 C.3 D.4
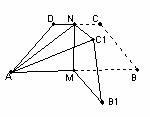
6.,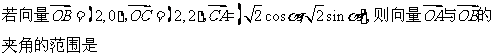
A.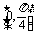 B.
B.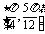 C.
C.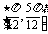 D.
D.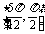
5.设不等式组 所表示的平面区域为Dn,记Dn的整数点个数为

A.2n B.2n+1 C.3n D.3n-1
4.节假日时,国人发手机短信问候亲友已成为一种时尚,若小李的40名同事中,给其发短信问候的概率为1,0.8,0.5,0的人数分别是8,15,14,3(人),通常情况下,小李应收到同事问候的信息条数为
A.27 B.37 C.38 D.8

3.设函数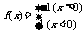 ,则
,则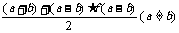 的值为
的值为
A.a B.b C.a、b中较小的数 D.a、b中较大的数
2.在算式:“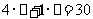 ”的两个
”的两个 中填入两个正整数,使它们的倒数之和最小,则这两个数构成的数对
中填入两个正整数,使它们的倒数之和最小,则这两个数构成的数对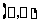 应为
应为
A.(4,4) B.(5,10) C.(3,18) D.(6,12)
1.已知i为虚数单位,则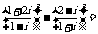
A.-3+4i B. 0 C.-4+3i D.-4-3i
17(12分)从4名男生和2名女生中任选3人参加演讲比赛,设随机变量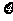 表示所选3人中女生的人数.
表示所选3人中女生的人数.
(Ⅰ)求 的分布列; (Ⅱ)求
的分布列; (Ⅱ)求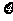 的数学期望;
的数学期望;
18(12分)数列an=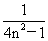 ,它的前n项和为Sn,求
,它的前n项和为Sn,求 Sn
Sn
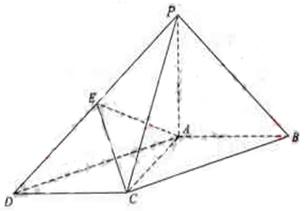 19(12分)如图,在底面为平行四边表的四棱锥
19(12分)如图,在底面为平行四边表的四棱锥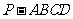 中,
中,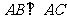 ,
,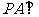 平面
平面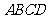 ,且
,且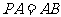 ,点
,点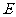 是
是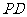 的中点.
的中点.
(Ⅰ)求证: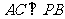 ;
;
(Ⅱ)求证: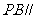 平面
平面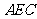 ;
;
(Ⅲ)求二面角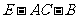 的大小.
的大小.
20(12分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量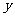 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度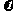 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: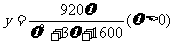 .
.
(1)在该时段内,当汽车的平均速度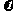 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
21(12分)已知椭圆中心在原点,焦点在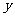 轴上,焦距为4,离心率为
轴上,焦距为4,离心率为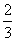 ,
,
(Ⅰ)求椭圆方程;
(Ⅱ)设椭圆在y轴正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段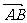 所成的比为2,求线段AB所在直线的方程。
所成的比为2,求线段AB所在直线的方程。
22(14分)数列{an}满足 .
.
(Ⅰ)用数学归纳法证明: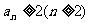 ;
;
(Ⅱ)已知不等式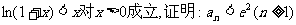 ,其中无理数
,其中无理数
e=2.71828….
14、棱长为3的正方体的顶点都在同一球面上,则该球的表面积为________.
15某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆。为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取 ,z , 辆。
16设函数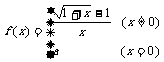 在
在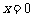 处连续,则实数
处连续,则实数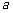 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com