
6.对于不重合的两条直线m,n和平面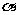 ,下列命题中的真命题是 ( )
,下列命题中的真命题是 ( )
A.如果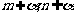 ,m,n是异面直线,那么
,m,n是异面直线,那么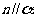
B.如果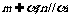 ,m,n是共面,那么
,m,n是共面,那么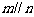
|
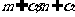 ,m,n是异面直线,那么
,m,n是异面直线,那么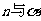 相交
相交
D.如果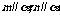 ,m,n共面,那么
,m,n共面,那么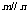
5.从4台A型笔记本电脑与5台B型笔记本电脑中任选3台,其中至少要有A型和B型笔记本电脑各一台,则不同的选取方法共有 ( )
A.140种 B.84种 C.70种 D.35种
4.光线沿直线y=2x+1射到直线y=x上,被直线y=x反射后的光线所在的直线方程为( )
A.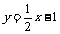 B.
B.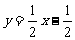 C.
C.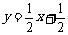 D.
D.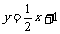
3.把函数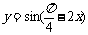 的图象向右平移
的图象向右平移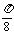 个单位,所得图象对应函数的最小正周期是( )
个单位,所得图象对应函数的最小正周期是( )
A.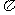 B.2
B.2 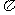 C.4
C.4 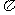 D.
D.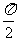
2.若复数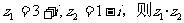 在复平面内对应的点位于 ( )
在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.设全集U={1,3,5,7,9},集合A={1,9,|a-5|},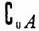 ={5,7},则a的值为( )
={5,7},则a的值为( )
A.2 B.8 C.-2或8 D.2或8
18.(14分)已知定点F(1,0),动点P在y轴(不含原点)上运动,过点P作线段PM交x轴于点M,使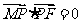 ;再延长线段MP到点N,使
;再延长线段MP到点N,使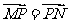 。
。
(Ⅰ)求动点N的轨迹C的方程;
(Ⅱ)直线L与轨迹C交于A、B两点,如果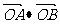 =-4且
=-4且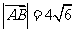 ,求直线L的方程。
,求直线L的方程。
(19)(14分)设函数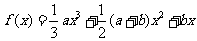 的图象过点(-1,2)。
的图象过点(-1,2)。
(Ⅰ)试用a表示b;
(Ⅱ)当a=3时,求f(x)的单调区间与极值;
(Ⅲ)若a<0且f(-1)是函数f(x)的极小值,求a的取值范围。
(20)(13分)已知数列{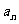 }满足
}满足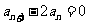 ,且
,且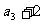 是
是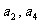 的等差中项。
的等差中项。
(Ⅰ)求数列{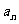 }的通项公式
}的通项公式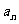 ;
;
(Ⅱ)若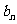 =
=
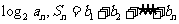 ,求使S
,求使S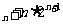 >50成立的正整数n的最小值。
>50成立的正整数n的最小值。
17.(14分)已知四棱锥S-ABCD的底面ABCD是正方形,SA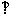 底面ABCD,点E是SC上的一点。
底面ABCD,点E是SC上的一点。
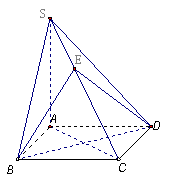 (Ⅰ)求证:平面EBD
(Ⅰ)求证:平面EBD 平面SAC;
平面SAC;
(Ⅱ)设SA=4,AB=2,求点A到平面SBD的距离;
(Ⅲ)当SA=AB时,求二面角B-SC-D的大小。
16.(12分)袋中黑白球共7个,从中任取2个球都是白球的概率为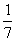 ,现有甲、乙两人从袋中轮流摸取1球,规定甲先乙后,然后甲再取…,取后不放回,直到两人中有一人取到白球就终止,每个球在每次被摸出的机会均等。
,现有甲、乙两人从袋中轮流摸取1球,规定甲先乙后,然后甲再取…,取后不放回,直到两人中有一人取到白球就终止,每个球在每次被摸出的机会均等。
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求甲取到白球的概率。
15.(13分)已知向量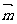 =(sin
=(sin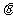 ,2cos
,2cos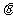 ),
),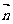 =(
=(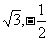 )
)
(Ⅰ)当qÎ[0,p]时,求函数f(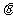 )=
)=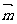 ×
×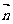 的值域;
的值域;
(Ⅱ)若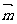 ∥
∥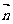 ,求sin2
,求sin2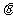 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com