
7.如图,程序框图所进行的求和运算是 ( )
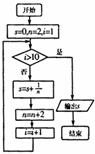 A.
A.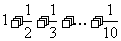
B.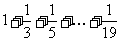
C.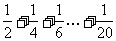
D.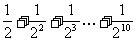
6.已知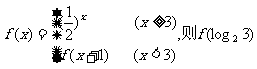 的值是 ( )
的值是 ( )
A.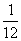 B.
B.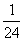
C.24 D.12
5.设F是椭圆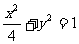 的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,
的右焦点,椭圆上的点与点F的最大距离为M,最小距离是m,
则椭圆上与点F的距离等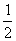 (M+m)的点的坐标是 ( )
(M+m)的点的坐标是 ( )
A.(0,±2) B.(0,±1) C.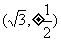 D.
D.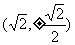
4.在一底面半径和高都是2m的圆柱形容器中盛满小麦种子,但有一粒带麦锈病的种子混入
了其中.现从中随机取出2m3的种子,则取出带麦锈病的种子的概率是 ( )
A.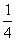 B.
B.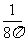 C.
C.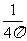 D.
D.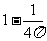
3.一个几何体的三视图如图所示,则该几何体的体积等于 ( )
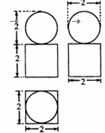 A.8+
A.8+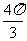
B.4+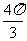
C.8+4π
D.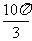
2.已知条件p:1≤x≤4,条件q:|x-2|>1,则p是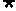 q的 ( )
q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
1.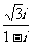 的共轭复数是 ( )
的共轭复数是 ( )
A.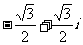 B.
B.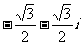 C.
C.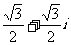 D.
D.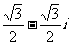
22.(本小题满分14分)
设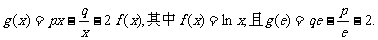 (e为自然对数的底数)
(e为自然对数的底数)
(Ⅰ)求p与q的关系;
(Ⅱ)若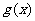 在其定义域内为单调函数,求p的取值范围;
在其定义域内为单调函数,求p的取值范围;
(Ⅲ)证明:
①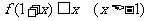 ;
;
②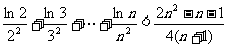 (n∈N,n≥2).
(n∈N,n≥2).
21.(本小题满分12分)
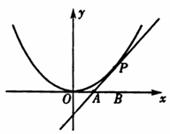
如图,已知直线l与抛物线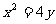 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(Ⅰ)若动点M满足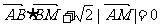 ,求点M的轨迹C;
,求点M的轨迹C;
(Ⅱ)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
20.(本小题满分12分)
某次象棋比赛的决赛在甲乙两名棋手之间举行,比赛采用积分制,比赛规则规定赢一局得2分,平一局得1分,输一局得0分,比赛共进行五局,积分有超过5分者比赛结束,否则继续进行,根据以往经验,每局甲赢的概率为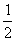 ,乙赢的概率为
,乙赢的概率为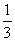 ,且每局比赛输赢互不影响,若甲第n局赢、平、输的得分分别记为an=2、an=1、an=0、n∈N*,1≤n≤5,令
,且每局比赛输赢互不影响,若甲第n局赢、平、输的得分分别记为an=2、an=1、an=0、n∈N*,1≤n≤5,令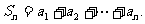
(Ⅰ)求S3 = 5的概率;
(Ⅱ)若随机变量ξ满足Sξ=7(ξ表示局数),求ξ的分布列和数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com