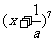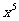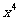(9) 在的展开式中，含与项的系数相等，则a的值是　　　　 .

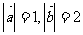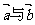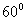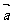(10) 已知向量，的夹角为，要使向量与垂直，则= .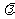

(11) 已知函数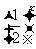y=与y=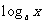(a>0且a¹1)，两者的图像相交于点P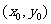，如果x₀³2,那么a的取值范围是　　　　 .

(12) 各棱长为a的正三棱柱的六个顶点都在同一个球面上，则此球的表面积为　　　 .

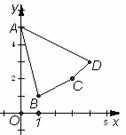(13) 如图，已知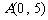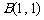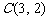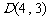，，，，动点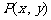所在的区域为四边形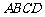(含边界)．若目标函数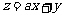只在点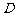处取得最优解，则实数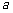的取值范围是________．

(14)正整数按下表排列：

1　 2　 5　 10　 17　 …

4　 3　 6　 11　 18　 …

9　 8　 7　 12　 19　 …

16　 15　 14　 13　 20　 …

25　 24　 23　 22　 21　 …

…　 …　 …　 …　 …　 …　

位于对角线位置的正整数1，3，7，13，21，…，构成数列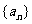，则a₇=_____；通项公式=　　　　　　 .

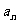　(1) 如果复数(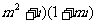是实数，则实数m是

(A) 1　　　　　　　 (B) －1　　　　　　 (C) 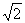　　　　　　　(D) －

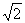
(2) 在底面是矩形的直四棱柱ABCD-A₁B₁C₁D₁中，∠DAD₁=∠CDC₁=45°，那么异面直线AD₁与DC₁所成角的度数为

(A)　 30°　　 (B)　 45°　　 (C)　 60°　　 (D)　 90°

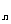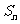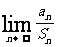(3) 设等比数列{a}为1，2，4，8，…，其前n项和为，则的值为

(A) 0　　　　　　　　　 (B) 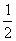　　　　　　　(C) 1　　　　　　　　 (D) 2

(4) 已知f(x)是R上的增函数，点A(－2，1)、B(2，3)在它的图像上，那么，不等式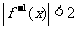的解集是

(A) {x│－1<x<1}　　 (B) {x│－2<x<2}　　 (C) {x│－2<x<3}　　 (D) {x│1<x<3}

(5) “a+b=2”是“直线x+y=0与圆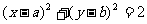相切”的

(A) 充分不必要条件　　　　　　　　　 (B) 必要不充分条件

(C) 充分必要条件　　　　　　　　　　 (D) 既不充分也不必要条件

(6) 把编号为1、2、3、4、5的5位运动员排在编号为1、2、3、4、5的5条跑道中，要求有且只有两位运动员的编号与其所在跑道的编号相同，共有不同的排法种数是

(A) 10　　　　　　　 (B) 20　　　　　　 (C) 40　　　　　　　　 (D) 60

(7) 已知M(2,1)，N(－1,2)，在下列方程的曲线上，存在点P满足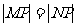的曲线方程是

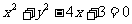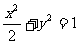(A) 3x－y+1=0　　 (B)　　 (C) 　　(D)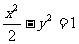

(8) 对任意两实数a、b，定义运算“”如下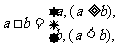：则关于函数f(x)=sinxcosx正确的命题是

(A) 函数f(x)值域为[－1，1]　　　

(B)当且仅当x=2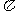k(k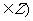时，函数f(x)取得最大值1

(C)函数f(x)的对称轴为x=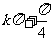(k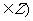

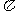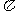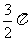(D)当且仅当2k<x<2k+(k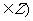时，函数f(x)<0

第Ⅱ卷(非选择题　 共110分)

20．(本小题满分14分)

　　　 已知双曲线的中心在原点O，右焦点为F ( c,0 )，P是双曲线右支上一点，且△OFP的面积为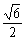

　　　 (Ⅰ)若点P坐标为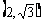，求此双曲线的离心率；

(Ⅱ)若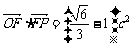，当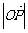取得最小值时，求此双曲线的方程。

19．(本小题满分14分)

　　　 已知数列{a_n}的前n项和为S_n，点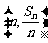在直线y = 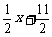上。数列{b_n}满足b_n+2 –2b_n+1 + b_n = 0 (n∈N*)，且b₃ = 11 ,前9项和为153 。

　　　 (Ⅰ)求数列{a_n}、{b_n}的通项公式；

(Ⅱ)设c_n =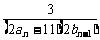，数列{c_n}的前n项和为T_n，求使不等式T_n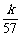＞对一切n∈N*都成立的最大正数k的值；

18．(本小题满分13分)

　　　 已知函数f ( x ) = x³ + ax² + bx + c 在x =1 处有极值，f ( x )在x = 2处的切线l不过第四象限且倾斜角为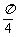，坐标原点到切线l的距离为。

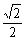　　　 (Ⅰ)a、b、c的值；

(Ⅱ)求函数y = f ( x )在区间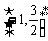上的最大值和最小值。

17．(本小题满分13分)

　　　 如图，棱长为1的正四面体ABCD中，E、F分别是棱AD、CD的中点，O是点A在平面BCD内的身影。

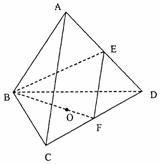
　　　 (Ⅰ)求直线EF与直线BC所成角的大小；

(Ⅱ)求点O到平面ACD的距离；

(Ⅲ)求二面角C-BF-E的大小。

16．(本小题满分13分)

　　　 甲、乙两支篮球队进行比赛，已知每一场甲队获胜的概率为0.6，乙队获胜的概率为0.4，每场比赛均要分出胜负。比赛是采用三场两胜制，即先取得两场胜利的球队胜出。

　　　 (Ⅰ)求甲队以二比一获胜的概率；

(Ⅱ)求乙获胜的概率；

15．(本小题满分13分)

　　　 已知向量a=(cosx,sinx), b =(–cosx,cosx )，函数f(x) =2a·b + 1

　　　 (Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)当x∈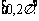时，求f(x)的单调减区间。

14．已知函数f ( x ) =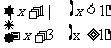　 则不等式f ( x )≥1的解集是_______。

三解答题：本大题共6小题，共80分。解答应写出文字说明、证明过程或演算步骤。

13．已知向量a = ( 2 , 3 ) ,| b | = 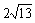,且a∥b，则| a | = ________ ，b的坐标是_________。