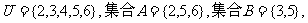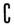1．已知全集则(_UB)∩A=　　 (　　 )

　　　 A．{5}　　　　　　　　　　 B．{2，6}　　　　　　　　 C．{2，3，4，6}　　 D．{3}

19．(本题满分13分)

　　　 已知椭圆C₁ 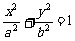：(a＞b＞0)的一条准线方程是x = 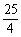,其左、右顶点分别是A、B双曲线C₂ 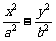：=1的一条渐近线方程为3x –5y = 0 .

　　　 (1)求椭圆C₁的方程及双曲线C₂的离心率；

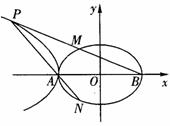
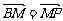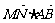　　　 (2)在第二象限内取双曲线C₂上一点， 连结BP交椭圆C₁于点M，连结PA并延长交椭圆C₁于点N，若。求证：= 0 。

20(本题满分13分)

　　　 设函数f ( x )的定义域、值域均为R，f ( x ) 反函数为f^–1 ( x ),且对任意实数x，均有f ( x ) + f^–1 ( x )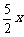＜。定义数列{a_n} : a₀ = 8 , a₁ = 10 , a_n = f (a_n–1 ) , n = 1, 2 , … .

　　　 (1)求证：a_n+1 + a_n–1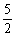＜a_n ( n = 1 , 2 , … ) ;

　　 (2)设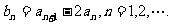求证：；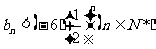

　　　 (3)是否存在常数A和B，同时满足；

　　　 ①当n = 0 及n = 1 时，有a_n =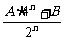成立；

②当n = 2 , 3, … 时，有a_n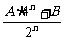＜成立。

　如果存在满足上述条件的实数A、B的值；如果不存在，证明你的结论。

18．(本题满分14分)

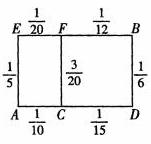
　　　 某先生居住城镇的A处，准备开车到单位B上班。若该路段生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图。(如图A→C→D算作两个路段：路段AC发生堵车事件的概率为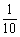，路段CD发生堵车事件的概率为。)

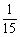　　　 (1)请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；

　　　 (2)若记路线A→C→F→B中遇到堵车次数为随机变量，求的数学期望E。

17．(本题满分13分)

　　　 已知三次波函数f ( x )的导函数为f′( x )，f′( 1 ) = 0 , f′(2 ) = 3 , f′( 3 ) = 12 .

　　　 (1)求f ( x ) – f ( 0 )的表达式；

　　　 (2)若对任意的x∈[ –1 , 4 ]，都有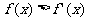成立，求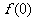的取值范围。

16．(本题满分14分)

　　　 在四棱锥P-ABCD中，底面ABCD是一直角梯形，∠BAD = 90°， AD∥BC，AB = BC = a ，AD = 2a , PA⊥底面ABCD，PD与底面成30°角。

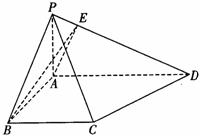
　　　 (1)若AE⊥PD，E为垂足，求证：BE⊥PD；

　　　 (2)在(1)的条件下，求异面直线AE与CD所成的角余弦值；

　　　 (3)求平面PAB与平面PCD所成的二面角的正切值。

15．(本题满分13分)

　　　 已知向量a = ( 1 – tan x , 1 ) , b = ( 1 + sin2x + cos2x , –3 ),记f ( x ) = a·b 。

　　　 (1)求f ( x )的定义域、值域和最小阶观测器正周期；

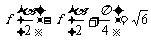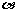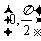　　　 (2)若，其中∈求。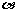

14．已知F₁、F₂分别是双曲线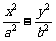=1(a＞0，b＞0)的左、右焦点，P为双曲线左支上任意一点，若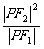的最小值为8a，则该双曲线离心率e的取值范围是_____________。

13．已知x、y满足(x – y –1)(x+y)≤0，则 ( x + 1 )² + ( y + 1 )²的最小的值______________.

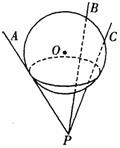
12．如图是根细铁杆PA、PB、PC组成的支架，三根杆的两两夹角都是60°，一个半径为1的球放在支架上，则球心O到点P的距离是__________

11．一次文艺演出中。需要给舞台上方安装一排完全相同的彩灯共15只，以不同的点亮方

式增加舞台效果，设计要求如下：每次点亮时，恰好有只是关的，且相邻的灯不同时被关掉，两端的灯必须点亮，那么不同的点亮方式的种数是_____________ 。(用数字作答)