
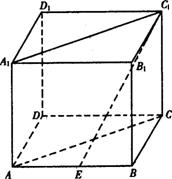
7.(理)正方体ABCD-A1B1C1D1中,若E为棱AB的中点,则直线C1E与平面ACC1A1所成角的正切值为( )
A.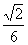 B.
B.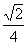 C.
C.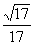 D.
D.
(文)设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n β,m⊥n
β,m⊥n α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β m⊥n
D.α⊥β,α∩β=m,m⊥n
m⊥n
D.α⊥β,α∩β=m,m⊥n n⊥β
n⊥β
6.(理)已知直线m,n和平面α,那么m∥n的一个必要但非充分条件是( )
A.m∥α,n∥α B.m⊥α,n⊥α
C.m∥α且n α
D.m,n与α成等角
α
D.m,n与α成等角
(文)函数f(x)=log3(x2-2x-8)的唯调减区间为( )
A.(-∞,1) B.(-∞,-2)
C.(4,+∞) D.(-∞,1]
5.(理)设m,n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是( )
A.m⊥α,n β,m⊥n
β,m⊥n α⊥β
B.α∥β,m⊥α,n∥β
α⊥β
B.α∥β,m⊥α,n∥β m⊥n
m⊥n
C.α⊥β,m⊥α,n∥β m⊥n D.α⊥β,α∩β=m,m⊥n
m⊥n D.α⊥β,α∩β=m,m⊥n n⊥β
n⊥β
(文)函数y= (-1≤x<0)的反函数是( )
(-1≤x<0)的反函数是( )
A.y=- (
( <x≤1)
B.y=-
<x≤1)
B.y=- (x≥
(x≥ )
)
C.y= (
( <x≤1)
D.y=
<x≤1)
D.y= (x≥
(x≥ )
)
4.(理)已知函数在f(x)=logsin1(x2-6x+5)在(a,+∞)上是减函数,则实数a的取值范围为( )
A.(5,+∞) B.[5,+∞)
C.(-∞,3) D.(3,+∞)
(文)定义在R上的函数y=f(x)的值域为[a,b],则y=f(x+1)的值域为( )
A.[a,b] B.[a+1,b+1]
C.[a-1,b-1] D.无法确定
3.(理)函数y= (-1≤x<0)的反函数是( )
(-1≤x<0)的反函数是( )
A.y=- (
( <x≤1)
B.y=-
<x≤1)
B.y=- (x≥
(x≥ )
)
C.y= (
( <x≤1)
D.y=
<x≤1)
D.y= (x≥
(x≥ )
)
(文)函数y= 的定义域是( )
的定义域是( )
A.(3,+∞) B.[3,+∞)
C.(4,+∞) D.[4,+∞)
2.(理)函数f(x)= +lg(3x+1)的定义域是( )
+lg(3x+1)的定义域是( )
A.(- ,+∞)
B.(-
,+∞)
B.(- ,1)
,1)
C.(- ,
, )
D.(-∞,-
)
D.(-∞,- )
)
(文)一个容量为20的样本数据,分组后,组别与频数如下:
|
组别 |
(10,20] |
(20,30] |
(30,40] |
(40,50] |
(50,60] |
(60,70] |
|
频数 |
2 |
3 |
4 |
5 |
4 |
2 |
则样本在(20,50]上的频率为( )
A.12% B.40% C.60% D.70%
1.(理)设f:x→x2是集合A到集合B的映射,如果B={1,2},则A∩B等于( )
A.{1}
B. C.
C. 或{1}
D.
或{1}
D. 或{2}
或{2}
(文)已知集合A={x|x2-5x+6≤0},集合B={x||2x-1|>3},则集合A∩B=( )
A.{x|2<x≤3} B.{x|2≤x<3}
C.{x|2≤x≤3} D.{x|-1<x<3}
22.(本小题满分l4分)
已知圆C的圆心在直线3x-y=0上,与x轴正半轴相切,且被直线x-y=0截得的弦长
为 .
.
(Ⅰ)求圆C的方程.
(Ⅱ)从圆C外一点P向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使
|PM|最小时点P的坐标.
21.(本小题满分l2分)
|
销售价(x元/台) |
35 |
40 |
45 |
50 |
|
日销售量(y台) |
57 |
42 |
27 |
l2 |
|
日销售额(t元) |
1995 |
|
|
|
|
日销售利润(p元) |
285 |
|
|
|
某商场经营一批进价为a元/台的小商品,经调查得知如下数据,若销售价上下调整,销售量和利润大体如下:

(I)在右面给出的直角坐标系中,根据表中的数
据描出实数对(x,y)的对应点,并写出y关于x的
一个函数关系式;
(Ⅱ)请把表中的空格里的数据填上;
(Ⅲ)根据表中的数据求p关于x的函数关系式,
并指出当销售单价为多少元时,才能获得最大日销售
利润?
20.(本小题满分12分)
已知△ABC中,顶点A(3,-1),AB边上的中线所在直线方程为6x+10y-59=0,∠B的
平分线所在直线方程为x-4y+l0=0.求:
(I)顶点启的坐标;
(Ⅱ)直线BC的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com