
(1)在等比数列{an}中,a2=8,a1=64,,则公比q为
(A)2 (B)3 (C)4 (D)8
(2)设全集U=|a、b、c、d|,A=|a、c|,B=|b|,则A∩(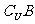 )=
)=
(A)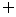 (B){a} (C){c} (D){a,c}
(B){a} (C){c} (D){a,c}
(3)垂直于同一平面的两条直线
(A)平行 (B)垂直 (C)相交 (D)异面
(4)(2x-1)2展开式中x2的系数为
(A)15 (B)60 (C)120 (D)240
(5)“-1<x<1”是“x2<1”的
(A)充分必要条件 (B)充分但不必要条件
(C)必要但不充分条件 (D)既不充分也不必要条件
(6)下列各式中,值为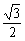 的是
的是
(A)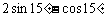 (B)
(B)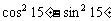
(C)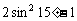 (D)
(D)
(7)从5张100元,3张200元,2张300元的奥运预赛门票中任取3张,则所取3张中至少有2张价格相同的概率为
(A)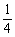 (B)
(B)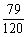 (C)
(C)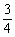 (D)
(D)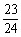
(8)若直线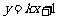 与圆
与圆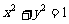 相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为
相交于P、Q两点,且∠POQ=120°(其中O为原点),则k的值为
(A) -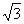 或
或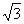 (B)
(B)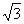 (C)
(C)
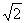 或
或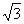 (D)
(D)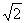
(9)已知向量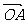 =(4,6),
=(4,6),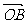 =(3,5),且
=(3,5),且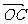 ⊥
⊥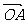 ,
,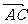 ∥
∥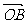 ,则向量
,则向量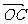 =
=
(A)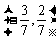 (B)
(B)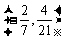 (C)
(C)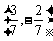 (D)
(D)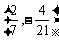
(10)设P(3,1)为二次函数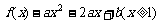 的图象与其反函数
的图象与其反函数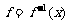 的图象的一个交点,则
的图象的一个交点,则
(A)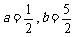 (B)
(B)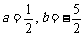
(C)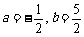 (D)
(D)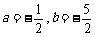
(11)设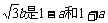 的等比中项,则a+3b的最大值为
的等比中项,则a+3b的最大值为
(A)1 (B)2 (C)3 (D)4
(12)已知以F1(2,0),F2(2,0)为焦点的椭圆与直线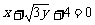 有且仅有一个交点,则椭圆的长轴长为
有且仅有一个交点,则椭圆的长轴长为
(A)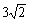 (B)
(B)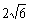 (C)
(C)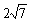 (D)
(D)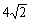
(17)(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为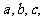
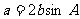
(Ⅰ)求B的大小;
(Ⅱ)求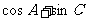 的取值范围.
的取值范围.
(18) (本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期为ζ的分布列为
|
ζ |
1 |
2 |
3 |
4 |
5 |
|
P |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,基利润为200元;分2期或3期付款,基利润为250元;分4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(Ⅰ)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率P(A);
(Ⅱ)求η的分布列及期Eη.
 (19)(本小题满分12分)
(19)(本小题满分12分)
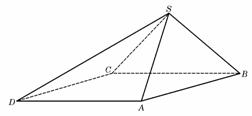
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2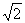 ,SA=SB=
,SA=SB=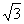 .
.
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.
(20)(本小题满分12分)
设函数f(x)=ex-e- x.
(Ⅰ)证明:f(x)的导数f'(x)≥2;
(Ⅱ)若对所有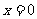 都有f(x)≥ax,求a的取值范围.
都有f(x)≥ax,求a的取值范围.
(21)(本小题满分12分)
已知椭圆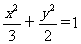 的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为(x0,y0),证明: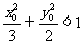 ;
;
(Ⅱ)求四过形ABCD的面积的最小值.
(22)(本小题满分12分)
已知数列{an}中a1=2,an+1=(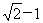 )(an+2),n=1,2,3….
)(an+2),n=1,2,3….
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中b1=2,bn+1=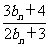 ,n=1,2,3,…,证明:
,n=1,2,3,…,证明:
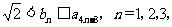 ….
….
(13)从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有 种.(用数字作答)
(14)函数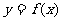 的图像与函数
的图像与函数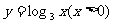 的图像关于直线
的图像关于直线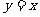 对称,则
对称,则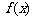 = _ .
= _ .
(15)等比数列{an}的前n项和Sn,已知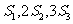 成等差数列,则{an}的公比为
.
成等差数列,则{an}的公比为
.
(16)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .
(1)a是第四象限角,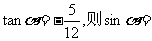
(A)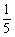 (B)
(B)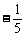 (C)
(C)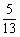 (D)
(D)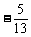
(2)设a是实数,且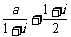 是实数,则a=
是实数,则a=
(A)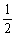 (B)1 (C)
(B)1 (C)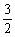 (D)2
(D)2
(3)已知向量a=(-5,6),b=(6,5),则a与b
(A)垂直 (B)不垂直也不平行
(C)平行且同向 (D)平行且反向
(4)已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为
(A)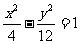 (B)
(B)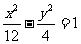
(C)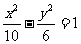 (D)
(D)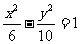
(5)设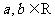 ,集合
,集合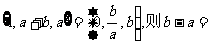
(1)1 (B)-1 (C)2 (D)-2
(6)下面给出的四个点中,到直线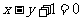 =0的距离为
=0的距离为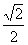 ,且位于
,且位于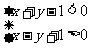 表示的平面区域内的点是
表示的平面区域内的点是
(A)(1,1) (B)(-1,1) (C)(-1,-1) (D)(1,-1)
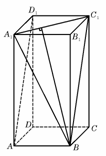
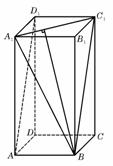 (7)如图,正四棱柱
(7)如图,正四棱柱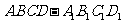 中,
中,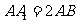 ,则异面直线
,则异面直线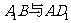 所成角的余弦值为
所成角的余弦值为
(A)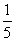
(B)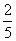
(C)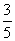
(D)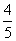
(8)设 ,函数
,函数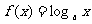 在区间
在区间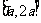 上的最大值与最小值之差为
上的最大值与最小值之差为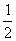 ,则
,则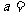
(A)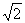 (B)2 (C)2
(B)2 (C)2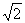 (D)4
(D)4
(9)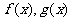 是定义在R上的函数,
是定义在R上的函数,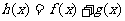 ,则“
,则“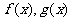 均为偶函数”是“
均为偶函数”是“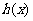 为偶函数”的
为偶函数”的
(A)充要条件 (B)充分而不必要的条件
(C)必要而不充分的条件 (D)既不充分也不必要的条件
(10)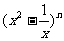 的展开式中,常数项为15,则
的展开式中,常数项为15,则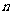 =
=
(A)3 (B)4 (C)5 (D)6
(11)抛物线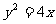 的焦点为
的焦点为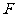 ,准线为
,准线为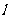 ,经过
,经过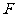 且斜率为
且斜率为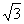 的直线与抛物线在
的直线与抛物线在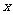 轴上方的部分相交于点
轴上方的部分相交于点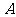 ,
,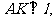 垂足为
垂足为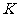 ,且△
,且△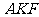 的面积是
的面积是
(A)4 (B)3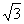 (C)4
(C)4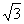 (D)8
(D)8
(12)函数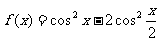 的一个单调增区间是
的一个单调增区间是
(A)(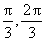 ) (B)(
) (B)(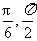 ) (C)(
) (C)(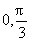 ) (D)(-
) (D)(-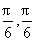 )
)
第Ⅱ卷(非选择题 共95分)
(17)(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA
(Ⅱ)求角B的大小;
(Ⅲ)若a=3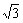 ,c=5,求b.
,c=5,求b.
(18)(本小题满分12分)
某商场经销某商品,顾客可采用一次性付款或分期付款购买.根据以往资料统计,顾客采用一次性付款的概率是0.6.经销一件该商品,若顾客采用一次性付款,商场获得利润200元;若顾客采用分期付款,商场获得利润250元.
(Ⅰ)求3位购买该商品的顾客中至少有1位采用一次性付款的概率;
(Ⅱ)求3位顾客每人购买1件该商品,商场获得利润不超过650元的概率.
(19)(本小题满分12分)
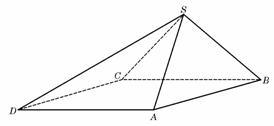 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2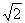 ,SA=SB=
,SA=SB=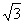 .
.
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.(20)(本小题满分12分)
设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的x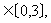 都有f(x)<c2成立,求c的取值范围.
都有f(x)<c2成立,求c的取值范围.
(21)(本小题满分12分)
设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13.
(Ⅰ)求{an},{bn}的通项公式;
(Ⅱ)求数列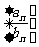 的前n项和Sn.
的前n项和Sn.
(22) (本小题满分12分)
已知椭圆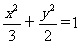 的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
的左、右焦点分别为F1、F2,过F1的直线交椭圆于B、D两点,过F2的直线交椭圆于A、C两点,且AC⊥BD,垂足为P.
(Ⅰ)设P点的坐标为(x0,y0),证明: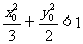 ;
;
(Ⅱ)求四过形ABCD的面积的最小值.
(13)从某自动包装机包装的食盐中,随机抽取20袋,测得各袋的质量分别为(单位:g):
492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5-501.5之间的概率约为
(14)函数y=f(x)的图像与函数y=log3x(x>0)的图像关于直线y=x对称,则f(x)=
(15)正四棱锥S-ABCD的底面边长和各测棱长都为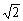 ,点S、A、B、C、D都在同一个球面上,则该球的体积为
,点S、A、B、C、D都在同一个球面上,则该球的体积为
(16)等比数列{an}的前n项和为Sn,已知S1,2S2,3S3成等差数列,则{an}的公比 .
(1)设S=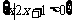 ,T=
,T=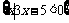 ,则S∩T=
,则S∩T=
(A)Ø
(B)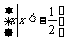
(C)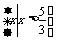 (D)
(D)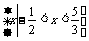
(2)α是第四象限角,cosα=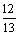 ,则sinα=
,则sinα=
(A)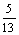 (B) -
(B) -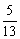 (C)
(C) 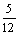 (D) -
(D) -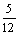
(3)已知向量a=(-5,6),b=(6,5),则a与b
(A)垂直 (B)不垂直也不平行
(C)平行且同向 (D)平行且反向
(4)已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为
(A)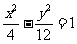 (B)
(B)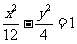
(C)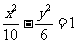 (C)
(C)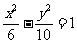
(5) 甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有
(A)36种 (B)48种 (C)96种 (D)192种
(6)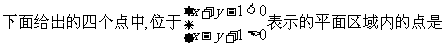
(A)(0,2) (B)(-2,0) (C)(0,-2) (D)(2,0)
(7)如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则异面直线A1B与AD1所成角的余弦值为
(A)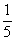 (B)
(B)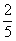 (C)
(C)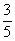 (D)
(D)
(8)设a>1,函数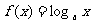 在区间[a,2a]上的最大值与最小值之差为
在区间[a,2a]上的最大值与最小值之差为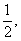 则a=
则a=
(A)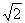 (B)2
(C)2
(B)2
(C)2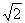 (D)4
(D)4
(9)f(x),g(x)是定义在R上的函数,h(x)=f(x)+ g(x),则“f(x),g(x)均为偶函数”,是“h(x)为偶数”的
(A)充分条件 (B)充分而不必要的条件
(C)必要而不充分的条件 (D)既不充分也不必要的条件
(10)函数y=2cos2x的一个单调增区间是
(A)(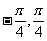 ) (B)(
) (B)(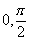 ) (C)(
) (C)(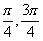 ) (D)(
) (D)(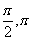 )
)
(11)曲线y=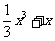 在点(1,
在点(1,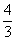 )处的切线与坐标轴围成的三角形面积为
)处的切线与坐标轴围成的三角形面积为
(A)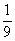 (B)
(B) 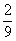 (C)
(C) 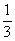 (D)
(D)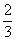
(12)抛物线y2=4x的焦点为F,准线为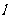 ,经过F且斜率为
,经过F且斜率为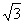 的直线与抛物线在
的直线与抛物线在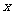 轴上方的部分相交于点A,AK⊥
轴上方的部分相交于点A,AK⊥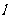 ,满足为K,则△AKF的面积是
,满足为K,则△AKF的面积是
(A)4
(B)3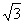 (C) 4
(C) 4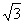 (D)8
(D)8
第Ⅱ卷
本卷共10题,共90分
22.已知函数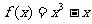
(1)求曲线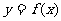 在点
在点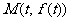 处的切线方程
处的切线方程
(2)设 ,如果过点
,如果过点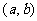 可作曲线
可作曲线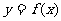 的三条切线,证明:
的三条切线,证明: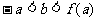
21.设数列{an}的首项a1∈ (0,1), an=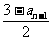 ,n=2,3,4…
,n=2,3,4…
(1)求{an}的通项公式;
(2)设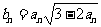 ,求证
,求证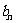 <
<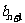 ,其中n为正整数。
,其中n为正整数。
20.在直角坐标系xOy中,以O为圆心的圆与直线: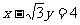 相切
相切
(1)求圆O的方程
(2)圆O与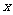 轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求
轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求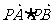 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com