
2.若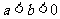 ,则下列不等式中不一定成立的是 ( )
,则下列不等式中不一定成立的是 ( )
A.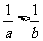 B.
B.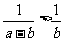 C.
C.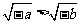 D.|a|>-b
D.|a|>-b
1.已知向量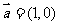 与向量
与向量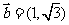 ,则向量
,则向量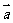 与
与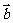 的夹角是 ( )
的夹角是 ( )
A.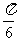
 B.
B.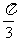 C.
C.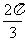 D.
D.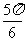
21.(本小题满分14分)
已知曲线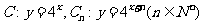 ,从
,从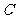 上的点
上的点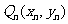 作
作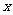 轴的垂线,交
轴的垂线,交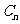 于点
于点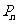 ,再从点
,再从点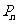 作
作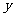 轴的垂线,交
轴的垂线,交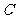 于点
于点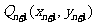 ,设
,设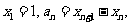
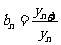 .
.
(1)求数列{xn}的通项公式;
(2)记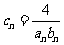 ,数列
,数列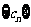 的前
的前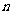 项和为Sn,试比较Sn与
项和为Sn,试比较Sn与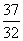 的大小
的大小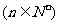 ;
;
(3)记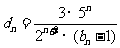 ,数列{dn}的前n项和为Tn,试证明:
,数列{dn}的前n项和为Tn,试证明:
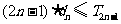
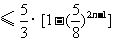 .
.
20.(本小题满分14分)
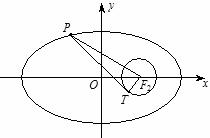
已知椭圆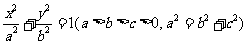 的左、右焦点分别为F1,F2,若以F2为圆心,
的左、右焦点分别为F1,F2,若以F2为圆心,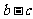 为半径作圆F2,过椭圆上一点
为半径作圆F2,过椭圆上一点 作此圆的切线,切点为
作此圆的切线,切点为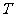 ,且|PT|的最小值不小于
,且|PT|的最小值不小于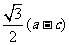 .
.
(1)求椭圆的离心率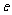 的取值范围;
的取值范围;
(2)设椭圆的短半轴长为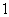 ,圆F2与x轴的右交点为Q,过点Q作斜率为k(k>0)的直线
,圆F2与x轴的右交点为Q,过点Q作斜率为k(k>0)的直线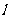 与椭圆相交于A,B两点,若
与椭圆相交于A,B两点,若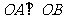 ,求直线l被圆F2截得的弦长s的最大值.
,求直线l被圆F2截得的弦长s的最大值.
19.(本小题满分13分)
已知函数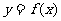 的反函数为
的反函数为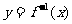 ,定义:若对给定的实数
,定义:若对给定的实数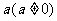 ,函数
,函数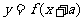 与
与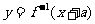 互为反函数,则称
互为反函数,则称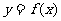 满足“a和性质”。
满足“a和性质”。
(1)判断函数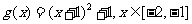 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)若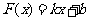 ,其中
,其中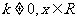 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得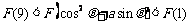 对任意的
对任意的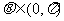 恒成立?若存在,求出a的范围;若不存在,请说明理由。
恒成立?若存在,求出a的范围;若不存在,请说明理由。
18.(本小题满分12分)
若关于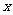 的实系数方程
的实系数方程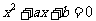 有两个根,一个根在区间(0,1)内,另一根在区间
有两个根,一个根在区间(0,1)内,另一根在区间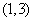 内,记点
内,记点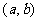 对应的区域为
对应的区域为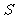 .
.
(1)设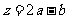 ,求
,求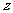 的取值范围;
的取值范围;
(2)过点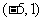 的一束光线,射到
的一束光线,射到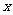 轴被反射后经过区域
轴被反射后经过区域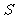 ,求反射光线所在直线
,求反射光线所在直线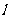 经过区域
经过区域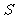 内的整点(即横纵坐标为整数的点)时直线
内的整点(即横纵坐标为整数的点)时直线 的方程.
的方程.
17.(本小题满分12分)
已知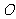 为坐标原点,向量
为坐标原点,向量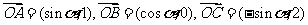 ,点
,点 是直线
是直线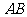 上的一点,且点
上的一点,且点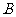 分有向线段
分有向线段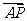 的比为
的比为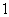 .
.
(1)记函数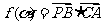 ,
,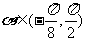 ,讨论函数
,讨论函数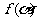 的单调性,并求其值域;
的单调性,并求其值域;
(2)若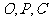 三点共线,求
三点共线,求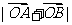 的值.
的值.
16.(本小题满分10分)
已知等比数列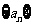 中,
中,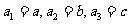 ,
,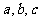 分别为
分别为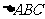 的三内角
的三内角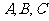 的对边,且
的对边,且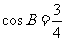 .
.
(1)求数列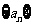 的公比
的公比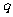 ;
;
(2)设集合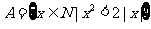 ,且
,且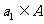 ,求数列
,求数列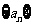 的通项公式.
的通项公式.
15.给出定义:若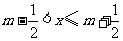 (其中
(其中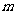 为整数),则m叫做离实数x最近的整数,记作
为整数),则m叫做离实数x最近的整数,记作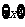 ,即
,即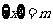 .在此基础上给出下列关于函数
.在此基础上给出下列关于函数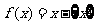 的四个命题:
的四个命题:
①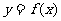 的定义域是
的定义域是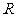 ,值域是
,值域是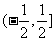 ;
;
②点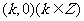 是
是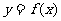 的图像的对称中心;
的图像的对称中心;
③函数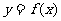 的最小正周期为1;
的最小正周期为1;
④函数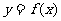 在
在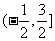 上是增函数;
上是增函数;
则其中真命题是_________.
14.若等差数列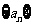 的前
的前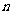 项和为
项和为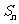 ,且
,且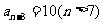 ,
,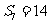 ,
,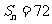 ,则_________.
,则_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com