
1.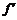 (x0)=
(x0)=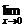
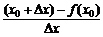 的几种等价形式:
的几种等价形式:
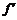 (x0)=
(x0)=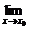
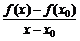
=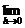
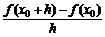
=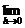
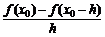
3.要注意含有参数的函数的导数的写法及研究在不定点处切线问题时切点的设法.
●教师下载中心
教学点睛
2.非多项式函数要化成多项式函数求导.
1.理解导数的定义及几何和物理方面的意义是解题的关键.
10.有点难度哟!
曲线y=x3+3x2+6x-10的切线中,求斜率最小的切线方程.
解: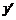 =3x2+6x+6=3(x+1)2+3,
=3x2+6x+6=3(x+1)2+3,
∴x=-1时,
切线最小斜率为3,此时,y=(-1)3+3×(-1)2+6(-1)-10=-14.
∴切线方程为y+14=3(x+1),即3x-y-11=0.
●思悟小结
9.确定抛物线方程y=x2+bx+c中的常数b和c,使得抛物线与直线y=2x在x=2处相切.
解: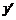 =2x+b,k=y′|x=2=4+b=2,
=2x+b,k=y′|x=2=4+b=2,
∴b=-2.
又当x=2时,y=22+(-2)×2+c=c,
代入y=2x,得c=4.
探究创新
8.有点难度哟!
若直线y=3x+1是曲线y=x3-a的一条切线,求实数a的值.
解:设切点为P(x0,y0),对y=x3-a求导数是
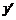 =3x2,∴3x02=3.∴x0=±1.
=3x2,∴3x02=3.∴x0=±1.
(1)当x=1时,
∵P(x0,y0)在y=3x+1上,
∴y=3×1+1=4,即P(1,4).
又P(1,4)也在y=x3-a上,
∴4=13-a.∴a=-3.
(2)当x=-1时,
∵P(x0,y0)在y=3x+1上,
∴y=3×(-1)+1=-2,即P(-1,-2).
又P(-1,-2)也在y=x3-a上,
∴-2=(-1)3-a.∴a=1.
综上可知,实数a的值为-3或1.
7.曲线y=-x2+4x上有两点A(4,0)、B(2,4).求:
(1)割线AB的斜率kAB及AB所在直线的方程;
(2)在曲线AB上是否存在点C,使过C点的切线与AB所在直线平行?若存在,求出C点的坐标;若不存在,请说明理由.
解:(1)kAB=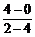 =-2,
=-2,
∴y=-2(x-4).
∴所求割线AB所在直线方程为2x+y-8=0.
(2)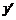 =-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
=-2x+4,-2x+4=-2,得x=3,y=-32+3×4=3.
∴C点坐标为(3,3),所求切线方程为2x+y-9=0.
6.点P在曲线y=x3-x+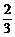 上移动,设点P处切线的倾斜角为
上移动,设点P处切线的倾斜角为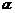 ,求
,求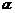 的范围.
的范围.
解:∵tan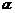 =3x2-1,
=3x2-1,
∴tan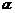 ∈[-1,+∞).
∈[-1,+∞).
当tan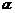 ∈[0,+∞)时,
∈[0,+∞)时,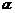 ∈[0,
∈[0,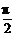 );
);
当tan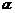 ∈[-1,0)时,
∈[-1,0)时,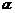 ∈[
∈[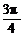 ,π).
,π).
∴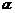 ∈[0,
∈[0,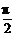 )∪[
)∪[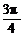 ,π).
,π).
培养能力
5.已知曲线y=x2-1与y=3-x3在x=x0处的切线互相垂直,求x0.
解:在x=x0处曲线y=x2-1的切线斜率为2x0,曲线y=3-x3的切线斜率为-3x02.
∵2x0·(-3x02)=-1,∴x0=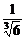 .
.
答案: 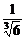
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com