
2.(2003年北京海淀区二模题)函数f(x)是定义域为R的偶函数,又是以2为周期的周期函数.若f(x)在[-1,0]上是减函数,那么f(x)在[2,3]上是
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
解析:∵偶函数f(x)在[-1,0]上是减函数,∴f(x)在[0,1]上是增函数.由周期为2知该函数在[2,3]上为增函数.
答案:A
1.定义在区间(-∞,+∞)上的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)上的图象与f(x)的图象重合,设a<b<0,给出下列不等式,其中成立的是
①f(b)-f(-a)>g(a)-g(-b)
②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a)
④f(a)-f(-b)<g(b)-g(-a)
A.①④ B.②③ C.①③ D.②④
解析:不妨取符合题意的函数f(x)=x及g(x)=|x|进行比较,或一般地g(x)=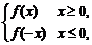 f(0)=0,f(a)<f(b)<0.
f(0)=0,f(a)<f(b)<0.
答案:D
5.给定函数:①y=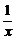 (x≠0);②y=x2+1;③y=2x;④y=log2x;⑤y=log2(x+
(x≠0);②y=x2+1;③y=2x;④y=log2x;⑤y=log2(x+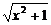 ).
).
在这五个函数中,奇函数是_________,偶函数是_________,非奇非偶函数是__________.
答案:①⑤ ② ③④
●典例剖析
[例1] 已知函数y=f(x)是偶函数,y=f(x-2)在[0,2]上是单调减函数,则
A.f(0)<f(-1)<f(2) B.f(-1)<f(0)<f(2)
C.f(-1)<f(2)<f(0) D.f(2)<f(-1)<f(0)
剖析:由f(x-2)在[0,2]上单调递减,
∴f(x)在[-2,0]上单调递减.
∵y=f(x)是偶函数,
∴f(x)在[0,2]上单调递增.
又f(-1)=f(1),故应选A.
答案:A
[例2] 判断下列函数的奇偶性:
(1)f(x)=|x+1|-|x-1|;
(2)f(x)=(x-1)·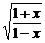 ;
;
(3)f(x)=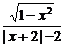 ;
;
(4)f(x)=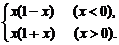
剖析:根据函数奇偶性的定义进行判断.
解:(1)函数的定义域x∈(-∞,+∞),对称于原点.
∵f(-x)=|-x+1|-|-x-1|=|x-1|-|x+1|=-(|x+1|-|x-1|)=-f(x),
∴f(x)=|x+1|-|x-1|是奇函数.
(2)先确定函数的定义域.由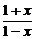 ≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.
≥0,得-1≤x<1,其定义域不对称于原点,所以f(x)既不是奇函数也不是偶函数.
(3)去掉绝对值符号,根据定义判断.
由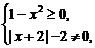 得
得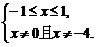
故f(x)的定义域为[-1,0)∪(0,1],关于原点对称,且有x+2>0.从而有f(x)= 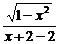 =
=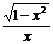 ,这时有f(-x)=
,这时有f(-x)=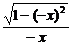 =-
=-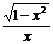 =-f(x),故f(x)为奇函数.
=-f(x),故f(x)为奇函数.
(4)∵函数f(x)的定义域是(-∞,0)∪(0,+∞),并且当x>0时,-x<0,
∴f(-x)=(-x)[1-(-x)]=-x(1+x)=-f(x)(x>0).
当x<0时,-x>0,∴f(-x)=-x(1-x)=-f(x)(x<0).
故函数f(x)为奇函数.
评述:(1)分段函数的奇偶性应分段证明.
(2)判断函数的奇偶性应先求定义域再化简函数解析式.
[例3] (2005年北京东城区模拟题)函数f(x)的定义域为D={x|x≠0},且满足对于任意x1、x2∈D,有f(x1·x2)=f(x1)+f(x2).
(1)求f(1)的值;
(2)判断f(x)的奇偶性并证明;
(3)如果f(4)=1,f(3x+1)+f(2x-6)≤3,且f(x)在(0,+∞)上是增函数,求x的取值范围.
(1)解:令x1=x2=1,有f(1×1)=f(1)+f(1),解得f(1)=0.
(2)证明:令x1=x2=-1,有f[(-1)×(-1)]=f(-1)+f(-1).解得f(-1)=0.
令x1=-1,x2=x,有f(-x)=f(-1)+f(x),∴f(-x)=f(x).∴f(x)为偶函数.
(3)解:f(4×4)=f(4)+f(4)=2,f(16×4)=f(16)+f(4)=3.
∴f(3x+1)+f(2x-6)≤3即f[(3x+1)(2x-6)]≤f(64).(*)
∵f(x)在(0,+∞)上是增函数,
∴(*)等价于不等式组
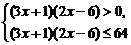
或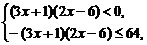
或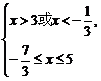 或
或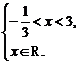
∴3<x≤5或-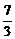 ≤x<-
≤x<-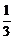 或-
或-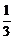 <x<3.
<x<3.
∴x的取值范围为{x|-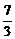 ≤x<-
≤x<-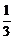 或-
或-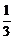 <x<3或3<x≤5}.
<x<3或3<x≤5}.
评述:解答本题易出现如下思维障碍:
(1)无从下手,不知如何脱掉“f”.解决办法:利用函数的单调性.
(2)无法得到另一个不等式.解决办法:关于原点对称的两个区间上,奇函数的单调性相同,偶函数的单调性相反.
深化拓展
已知f(x)、g(x)都是奇函数,f(x)>0的解集是(a2,b),g(x)>0的解集是(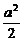 ,
,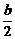 ),
),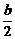 >a2,那么f(x)·g(x)>0的解集是
>a2,那么f(x)·g(x)>0的解集是
A.(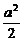 ,
,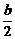 ) B.(-b,-a2)
) B.(-b,-a2)
C.(a2,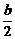 )∪(-
)∪(-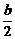 ,-a2) D.(
,-a2) D.(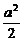 ,b)∪(-b2,-a2)
,b)∪(-b2,-a2)
提示:f(x)·g(x)>0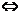
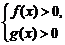 或
或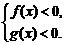
∴x∈(a2,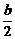 )∪(-
)∪(-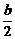 ,-a2).
,-a2).
答案:C
[例4] (2004年天津模拟题)已知函数f(x)=x+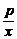 +m(p≠0)是奇函数.
+m(p≠0)是奇函数.
(1)求m的值.
(2)(理)当x∈[1,2]时,求f(x)的最大值和最小值.
(文)若p>1,当x∈[1,2]时,求f(x)的最大值和最小值.
解:(1)∵f(x)是奇函数,
∴f(-x)=-f(x).
∴-x-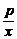 +m=-x-
+m=-x-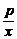 -m.
-m.
∴2m=0.∴m=0.
(2)(理)(ⅰ)当p<0时,据定义可证明f(x)在[1,2]上为增函数.∴f(x)max=
f(2)=2+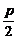 ,f(x)min=f(1)=1+p.
,f(x)min=f(1)=1+p.
(ⅱ)当p>0时,据定义可证明f(x)在(0,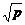 ]上是减函数,在[
]上是减函数,在[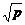 ,+∞)上是增函数.
,+∞)上是增函数.
①当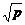 <1,即0<p<1时,f(x)在[1,2]上为增函数,
<1,即0<p<1时,f(x)在[1,2]上为增函数,
∴f(x)max=f(2)=2+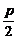 ,f(x)min=f(1)=1+p.
,f(x)min=f(1)=1+p.
②当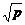 ∈[1,2]时,f(x)在[1,p]上是减函数.在[p,2]上是增函数.
∈[1,2]时,f(x)在[1,p]上是减函数.在[p,2]上是增函数.
f(x)min=f(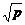 )=2
)=2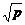 .
.
f(x)max=max{f(1),f(2)}=max{1+p,2+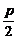 }.
}.
当1≤p≤2时,1+p≤2+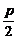 ,f(x)max=f(2);当2<p≤4时,1+p≥2+
,f(x)max=f(2);当2<p≤4时,1+p≥2+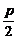 ,f(x)max=f(1).
,f(x)max=f(1).
③当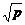 >2,即p>4时,f(x)在[1,2]上为减函数,∴f(x)max=f(1)=1+p,f(x)min=f(2)=2+
>2,即p>4时,f(x)在[1,2]上为减函数,∴f(x)max=f(1)=1+p,f(x)min=f(2)=2+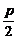 .
.
(文)解答略.
评述:f(x)=x+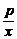 (p>0)的单调性是一重要问题,利用单调性求最值是重要方法.
(p>0)的单调性是一重要问题,利用单调性求最值是重要方法.
深化拓展
f(x)=x+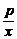 的单调性也可根据导函数的符号来判断,本题如何用导数来解?
的单调性也可根据导函数的符号来判断,本题如何用导数来解?
●闯关训练
夯实基础
4.已知f(x)=ax2+bx+3a+b是偶函数,且其定义域为[a-1,2a],则a=___________,b=___________.
解析:定义域应关于原点对称,
故有a-1=-2a,得a=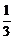 .
.
又对于所给解析式,要使f(-x)=f(x)恒成立,应b=0.
答案: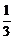 0
0
3.若偶函数f(x)在区间[-1,0]上是减函数,α、β是锐角三角形的两个内角,且α≠β,则下列不等式中正确的是
A.f(cosα)>f(cosβ) B.f(sinα)>f(cosβ)
C.f(sinα)>f(sinβ) D.f(cosα)>f(sinβ)
解析:∵偶函数f(x)在区间[-1,0]上是减函数,∴f(x)在区间[0,1]上为增函数.由α、β是锐角三角形的两个内角,
∴α+β>90°,α>90°-β.1>sinα>cosβ>0.
∴f(sinα)>f(cosβ).
答案:B
2.已知函数f(x)=ax2+bx+c(a≠0)是偶函数,那么g(x)=ax3+bx2+cx是
A.奇函数 B.偶函数
C.既奇且偶函数 D.非奇非偶函数
解析:由f(x)为偶函数,知b=0,有g(x)=ax3+cx(a≠0)为奇函数.
答案:A
1.下面四个结论中,正确命题的个数是
①偶函数的图象一定与y轴相交 ②奇函数的图象一定通过原点 ③偶函数的图象关于y轴对称 ④既是奇函数,又是偶函数的函数一定是f(x)=0(x∈R)
A.1 B.2 C.3 D.4
解析:①不对;②不对,因为奇函数的定义域可能不包含原点;③正确;④不对,既是奇函数又是偶函数的函数可以为f(x)=0(x∈(-a,a)).
答案:A
3.奇、偶函数的性质
(1)具有奇偶性的函数,其定义域关于原点对称(也就是说,函数为奇函数或偶函数的必要条件是其定义域关于原点对称).
(2)奇函数的图象关于原点对称,偶函数的图象关于y轴对称.
(3)若奇函数的定义域包含数0,则f(0)=0.
(4)奇函数的反函数也为奇函数.
(5)定义在(-∞,+∞)上的任意函数f(x)都可以唯一表示成一个奇函数与一个偶函数之和.
●点击双基
2.偶函数:对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x)(或f(x)-f(-x)=0),则称f(x)为偶函数.
1.奇函数:对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x)(或f(x)+ f(-x)=0),则称f(x)为奇函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com