
2.了解函数的单调性的概念,掌握判断一些简单函数的单调性的方法.
1.理解函数的概念,了解映射的概念.
4.直线与曲线相切,并不一定只有一个公共点,当曲线是二次曲线时,由解析几何知,直线与曲线相切,有且只有一个公共点,即切点.
拓展题例
[例题] 曲线y=x2+1上过点P的切线与曲线y=-2x2-1相切,求点P的坐标.
解:设P(x0,y0),由题意知曲线y=x2+1在P点的切线斜率为k=2x0,切线方程为y=2x0x+1-x02,而此直线与曲线y=-2x2-1相切,
∴切线与曲线只有一个交点,即方程2x2+2x0x+2-x02=0的判别式
Δ=4x02-2×4×(2-x02)=0.
解得x0=±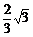 ,y0=
,y0=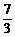 .
.
∴P点的坐标为(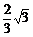 ,
,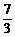 )或(-
)或(-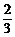
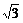 ,
,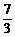 ).
).
3.若质点的运动规律为s=s(t),则质点在t=t0时的瞬时速度为v=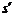 (t0).这就是导数的物理意义.
(t0).这就是导数的物理意义.
2.曲线C:y=f(x)在其上一点P(x0,f(x0))处的切线方程为
y-f(x0)=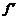 (x0)(x-x0).
(x0)(x-x0).
1.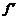 (x0)=
(x0)=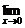
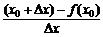 的几种等价形式:
的几种等价形式:
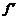 (x0)=
(x0)=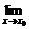
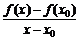
=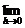
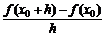
=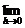
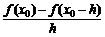
3.要注意含有参数的函数的导数的写法及研究在不定点处切线问题时切点的设法.
●教师下载中心
教学点睛
2.非多项式函数要化成多项式函数求导.
1.理解导数的定义及几何和物理方面的意义是解题的关键.
10.有点难度哟!
曲线y=x3+3x2+6x-10的切线中,求斜率最小的切线方程.
解: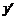 =3x2+6x+6=3(x+1)2+3,
=3x2+6x+6=3(x+1)2+3,
∴x=-1时,
切线最小斜率为3,此时,y=(-1)3+3×(-1)2+6(-1)-10=-14.
∴切线方程为y+14=3(x+1),即3x-y-11=0.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com